题目内容
8．若点（16，tanθ）在函数y=log2x的图象上，则$\frac{1+cos2θ+8si{n}^{2}θ}{sin2θ}$=（ ）| A． | $\frac{20\sqrt{3}}{3}$ | B． | $\frac{65}{4}$ | C． | 4 | D． | 4$\sqrt{2}$ |
分析 先根据对数的运算性质求出tanθ，再化简代值计算即可．
解答 解：点（16，tanθ）在函数y=log2x的图象上，
∴tanθ=log216=4，
∴$\frac{1+cos2θ+8si{n}^{2}θ}{sin2θ}$=$\frac{co{s}^{2}θ+4si{n}^{2}θ}{sinθcosθ}$=$\frac{1+4ta{n}^{2}θ}{tanθ}$=$\frac{1+4×{4}^{2}}{4}$=$\frac{65}{4}$，
故选：B．
点评 本题考查了二倍角公式，函数值的求法，以及对数的运算性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
16．已知i虚数单位，则（$\frac{1+2i}{1-i}$）2-（$\frac{2-i}{1+i}$）2=（ ）
| A． | -3+4i | B． | 0 | C． | -4+3i | D． | -4-3i |
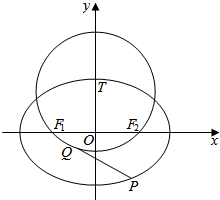如图，在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（1，$\frac{\sqrt{2}}{2}$），离心率e=$\frac{\sqrt{2}}{2}$，F1、F2为椭圆的左、右焦点．
13．设a为正实数，则“a≥1”是“$a+\frac{1}{a}≥2$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
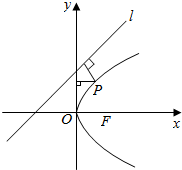已知直线l1：4x-3y+6=0和直线l2：x=0，抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是（ ）