题目内容
已知M={x|y=log2(1-x)(x+1)},N={y|y=x3+x,x∈[0,1]},则M∩N=
[0,1)
[0,1)
.分析:由对数式的真数大于0化简集合M,利用函数单调性化简集合N,然后利用交集运算求解.
解答:解:由(1-x)(x+1)>0,得-1<x<1.
∴M={x|y=log2(1-x)(x+1)}=(-1,1).
∵y=x3+x在x∈[0,1]上为增函数,
∴y∈[0,2].
∴N={y|y=x3+x,x∈[0,1]}=[0,2].
∴M∩N=[0,1).
故答案为[0,1).
∴M={x|y=log2(1-x)(x+1)}=(-1,1).
∵y=x3+x在x∈[0,1]上为增函数,
∴y∈[0,2].
∴N={y|y=x3+x,x∈[0,1]}=[0,2].
∴M∩N=[0,1).
故答案为[0,1).
点评:本题考查了对数函数的定义域的求法,考查了利用函数的单调性求解函数值域,考查了交集及其运算,是基础题.

练习册系列答案
相关题目
 .
. :x+2y-4=0相交于M,N两点,且
:x+2y-4=0相交于M,N两点,且 =
=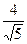 ,求m的值。
,求m的值。 .
. =
= ,求m的值。
,求m的值。