题目内容
已知函数f(x)=ax2+(b-8)x-a-ab,当x∈(-3,2)时,f(x)>0,当x∈(-∞,-3)∪(2,+∞)时,f(x)<0.
(1)求f(x)在[0,1]内的值域;
(2)c为何值时,ax2+bx+c≤0的解集为R?
(1)求f(x)在[0,1]内的值域;
(2)c为何值时,ax2+bx+c≤0的解集为R?
分析:由题意可得当x=-3和x=2时,有y=0,代入可求a,b,进而可求f(x)
(1)由二次函数的性质可判断其在[0,1]上的单调性,进而可求函数的值域
(2)令g(x)=-3x2+5x+c,要使g(x)≤0的解集为R.则△≤0,解不等式可求
(1)由二次函数的性质可判断其在[0,1]上的单调性,进而可求函数的值域
(2)令g(x)=-3x2+5x+c,要使g(x)≤0的解集为R.则△≤0,解不等式可求
解答:解:由题意知f(x)的图象是开口向下,交x轴于两点A(-3,0)和B(2,0)的抛物线,
对称轴方程为x=-
(如图).
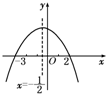
那么,当x=-3和x=2时,有y=0,代入原式得
∴
或
经检验a=0,b=8不符合题意,舍去.
∴f(x)=-3x2-3x+18.
(1)由图象知,函数在[0,1]内单调递减,
所以,当x=0时,y=18,当x=1时,y=12.
∴f(x)在[0,1]内的值域为[12,18].
(2)令g(x)=-3x2+5x+c,
要使g(x)≤0的解集为R.
则需要方程-3x2+5x+c=0的根的判别式△≤0,
即△=25+12c≤0,解得c≤-
.
∴当c≤-
时,ax2+bx+c≤0的解集为R.
对称轴方程为x=-
| 1 |
| 2 |

那么,当x=-3和x=2时,有y=0,代入原式得
|
∴
|
|
经检验a=0,b=8不符合题意,舍去.
∴f(x)=-3x2-3x+18.
(1)由图象知,函数在[0,1]内单调递减,
所以,当x=0时,y=18,当x=1时,y=12.
∴f(x)在[0,1]内的值域为[12,18].
(2)令g(x)=-3x2+5x+c,
要使g(x)≤0的解集为R.
则需要方程-3x2+5x+c=0的根的判别式△≤0,
即△=25+12c≤0,解得c≤-
| 25 |
| 12 |
∴当c≤-
| 25 |
| 12 |
点评:本题主要考查了二次函数、二次方程及二次不等式之间的关系的相互转化,二次函数性质的应用及二次不等式的求解,属于知识的简单应用

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目