题目内容
1.函数f(x)的图象如图所示,下列数值排序正确的是( )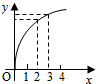
| A. | 0<f(3)-f(2)<f′(2)<f′(3) | B. | 0<f′(2)<f′(3)<f(3)-f(2) | C. | 0<f′(3)<f(3)-f(2)<f′(2) | D. | 0<f′(3)<f′(2)<f(3)-f(2) |
分析 观察图象及导数的几何意义得,即函数在(2,3)上增长得越来越慢,所以导数值为正,且绝对值越来越小,故f′(2)>f′(3),同时根据割线的性质,一定可以在(2,3)之间找到一点其切线的斜率等于割线斜率,即其导数值等于割线的斜率,由此可得结论.
解答 解:观察图象可知,该函数在(2,3)上为连续可导的增函数,且增长的越来越慢.
所以各点处的导数在(2,3)上处处为正,且导数的值逐渐减小,所以故f′(2)>f′(3),
而f(3)-f(2)=$\frac{f(3)-f(2)}{3-2}$,表示的连接点(2,f(2))与点(3,f(3))割线的斜率,根据导数的几何意义,一定可以在(2,3)之间找到一点,该点处的切线与割线平行,则割线的斜率就是该点处的切线的斜率,即该点处的导数,则必有:$0<f′(3)<\frac{f(3)-f(2)}{3-2}<f′(2)$.
故选:C.
点评 本题考查了函数的导数与函数单调性的关系,以及割线与切线间的关系,要注意数形结合来解题.

练习册系列答案
相关题目
9.已知集合A={-1,0,1},B={x|x+1>0},那么A∩B=( )
| A. | {-1,0,1} | B. | {0,1} | C. | (-1,+∞) | D. | [-1,+∞) |
6.设全集U=R,集合M={x|x>1},P={x|x2>1},则下列关系中正确的是( )
| A. | M=P | B. | P?M | C. | M?P | D. | ∁U(M∪P)=∅ |
10.定义运算(a,b)※(c,d)=ac-bd,则符合条件(z,1+2i)※(1+i,1-i)=0的复数z所对应的点在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
11.若函数f(x)=$\frac{1}{a{x}^{2}+bx+c}$的部分图象如图所示,则abc=( )
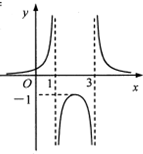

| A. | 12 | B. | -12 | C. | 8 | D. | -8 |