题目内容

10．定义运算（a，b）※（c，d）=ac-bd，则符合条件（z，1+2i）※（1+i，1-i）=0的复数z所对应的点在（　　）
A．第四象限B．第三象限C．第二象限D．第一象限

分析 由新定义列式，利用复数代数形式的乘除运算化简z，求出z的坐标得答案．

解答 解：由新定义（a，b）※（c，d）=ac-bd，得
（z，1+2i）※（1+i，1-i）=z（1+i）-（1+2i）（1-i）=0，
即z（1+i）=（1+2i）（1-i）=3+i，
∴$z=\frac{3+i}{1+i}=\frac{（3+i）（1-i）}{（1+i）（1-i）}=\frac{4-2i}{2}=2-i$．
∴复数z所对应的点的坐标为（2，-1），在第四象限．
故选：A．

点评 本题考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案
相关题目
20．已知如图是一个空间几何体的三视图，则该几何体的外接球的表面积为（　　）
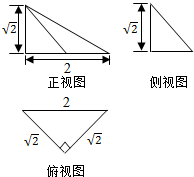
A．24πB．6πC．4πD．2π
1．函数f（x）的图象如图所示，下列数值排序正确的是（　　）
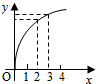
A．0＜f（3）-f（2）＜f′（2）＜f′（3）B．0＜f′（2）＜f′（3）＜f（3）-f（2）C．0＜f′（3）＜f（3）-f（2）＜f′（2）D．0＜f′（3）＜f′（2）＜f（3）-f（2）
18．设i是虚数单位，复数z=$\frac{2i}{1+i}$，则|z|=（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2
5．在某次联考数学测试中，学生成绩ξ服从正态分布（100，σ2），（σ＞0），若ξ在（80，120）内的概率为0.8，则落在（0，80）内的概率为（　　）
A．0.05B．0.1C．0.15D．0.2
15．已知函数f（x）=2ex，函数g（x）=k（x+1），若函数f（x）图象恒在函数g（x）图象的上方（没有交点），则实数的取值范围是（　　）
A．k＞2B．k≥2C．0≤k≤2D．0≤k＜2
2．复数$\frac{3+i}{1-3i}$=（　　）
A．-iB．iC．2iD．-2i
19．已知点$A（3，\sqrt{3}）$，O为坐标原点，点P（x，y）满足$\left\{{\begin{array}{l}{\sqrt{3}x-y≤0}\\{x-\sqrt{3}y+2≥0}\\{y≥0}\end{array}}\right.$，则满足条件点P所形成的平面区域的面积为$\sqrt{3}$，$\frac{{\overrightarrow{OA}•\overrightarrow{OP}}}{{|\overrightarrow{OA}|}}$的最大值是$\sqrt{3}$．
20．已知直线l1：ax+2y+6=0，l2：x+（a-1）y+a2-1=0，若l1⊥l2，则a=$\frac{2}{3}$，若l1∥l2，则a=-1，此时l1和l2之间的距离为$\frac{6\sqrt{5}}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网