题目内容
16．已知直线kx+2y+1=0，其方向向量为（2，-1），则k的值为1．分析 利用直线的平行向量与斜率的关系即可得出．
解答 解：∵直线kx+2y+1=0的斜率为-$\frac{k}{2}$，
平行向量（2，-1），
∴$-\frac{k}{2}$=-$\frac{1}{2}$，解得k=1．
故答案为：1．
点评 本题考查了直线的平行向量与斜率的关系，属于基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
4．已知p：|x|＜2；q：x2-x-2＜0，则p是q的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．已知平面向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=|$\overrightarrow b$|=1，（$\overrightarrow a$+2$\overrightarrow b$）（$\overrightarrow a$-$\overrightarrow b$）=-$\frac{1}{2}$，则与$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
1．函数f（x）的图象如图所示，下列数值排序正确的是（ ）
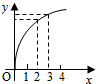
| A． | 0＜f（3）-f（2）＜f′（2）＜f′（3） | B． | 0＜f′（2）＜f′（3）＜f（3）-f（2） | C． | 0＜f′（3）＜f（3）-f（2）＜f′（2） | D． | 0＜f′（3）＜f′（2）＜f（3）-f（2） |
8．若△ABC中，cosA=$\frac{5}{13}$，cosB=$\frac{4}{5}$，则cosC的值为（ ）
| A． | $\frac{56}{65}$ | B． | -$\frac{56}{65}$ | C． | -$\frac{16}{65}$ | D． | $\frac{16}{65}$ |
5．在某次联考数学测试中，学生成绩ξ服从正态分布（100，σ2），（σ＞0），若ξ在（80，120）内的概率为0.8，则落在（0，80）内的概率为（ ）
| A． | 0.05 | B． | 0.1 | C． | 0.15 | D． | 0.2 |
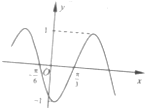设ω＞0，函数y=sin（ωx+φ）（-π＜φ＜π）的图象向左平移$\frac{π}{3}$个单位长度后，得到如图所示的图象，则ω=2，φ=$\frac{2π}{3}$．