题目内容
关于二次函数学生甲有以下观点:①二次函数必有最大值;②二次函数必有最小值;③闭区间上的二次函数必定同时存在最大值,最小值;④对于命题③,最值一定在区间端点取得.你认为学生甲正确的观点序号是
______.根据你的判断试解决下述问题:已知函数f(x)=ax2+(2a-1)x+1在[-
,2]上的最大值为3,求实数a的值.
| 3 |
| 2 |
(1)③(2分)
(2)当a=0时,f(x)=-x+1在[-
,2]上的最大值为
f(-
) =
≠3不合题意,舍去;(3分)
当a≠0时,
①令f(-
) =3得a=-
,此时抛物线开口向下,对称轴x=-2,
且-2∉[-
,2],故a= -
不合题意,舍去;(6分)
②令f(2)=3,得a=
,此时抛物线开口向上,
闭区间的右端点距离对称轴较远,故a=
符合题意;(9分)
③若f(-
) =3得a=-
经检验符合题意,(12分)
综上可知:实数a的值为a=
或a=-
(13分)
(2)当a=0时,f(x)=-x+1在[-
| 3 |
| 2 |
f(-
| 3 |
| 2 |
| 5 |
| 2 |
当a≠0时,
①令f(-
| 2a-1 |
| 2a |
| 1 |
| 2 |
且-2∉[-
| 3 |
| 2 |
| 1 |
| 2 |
②令f(2)=3,得a=
| 1 |
| 2 |
闭区间的右端点距离对称轴较远,故a=
| 1 |
| 2 |
③若f(-
| 3 |
| 2 |
| 2 |
| 3 |
综上可知:实数a的值为a=
| 1 |
| 2 |
| 2 |
| 3 |

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
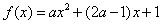 在
在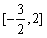 上的最大值为3,求实数a的值。
上的最大值为3,求实数a的值。 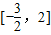 上的最大值为3,求实数a的值.
上的最大值为3,求实数a的值.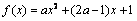 在
在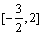 上的最大值为3, 求实数a的值.
上的最大值为3, 求实数a的值.