题目内容
设函数 在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是
在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是
| A.f (a+1)= f (2) | B.f (a+1)> f (2) |
| C.f (a+1)< f (2) | D.不确定 |
B
解析试题分析:结合对数函数的单调性的性质,由于函数 在(0,+∞)上单调递增,那么说明底数a>1,因此a+1>2,那么对于对数函数而言,那么变量大的函数值必然要大,由于a+1>2,则可知函数值满足f (a+1)> f (2),选B.
在(0,+∞)上单调递增,那么说明底数a>1,因此a+1>2,那么对于对数函数而言,那么变量大的函数值必然要大,由于a+1>2,则可知函数值满足f (a+1)> f (2),选B.
考点:本试题考查了函数的单调性的运用。
点评:解决该试题的关键是利用函数的单调性,来确定出参数a的范围,然后结合其性质来判定函数值的大小关系,属于基础题。

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,给出下列命题:
上的奇函数,给出下列命题: ;
; 上有最小值 -1,则
上有最小值 -1,则 上有最大值1;
上有最大值1; 上为减函数;
上为减函数; 时,
时, ; 则
; 则 时,
时, 。
。 ,给出下列四个说法:
,给出下列四个说法: ,则
,则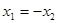 ,②点
,②点 是
是 的一个对称中心,
的一个对称中心, 上是增函数,④
上是增函数,④ 对称.
对称. 的定义域为 。
的定义域为 。 在其定义域内的一个子区间
在其定义域内的一个子区间 内不是单调函数,则实数k的取值范围_______________.
内不是单调函数,则实数k的取值范围_______________.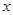 的方程
的方程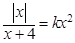 有四个不同的实数解,则
有四个不同的实数解,则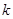 的取值范围是 .
的取值范围是 . ,则
,则 ;
; 的定义域是____________.
的定义域是____________.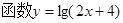 的定义域是
的定义域是