题目内容
若关于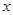 的方程
的方程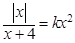 有四个不同的实数解,则
有四个不同的实数解,则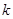 的取值范围是 .
的取值范围是 .
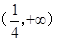
解析试题分析:由于关于x的方程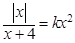 有四个不同的实根,x=0是此方程的1个根,
有四个不同的实根,x=0是此方程的1个根,
故关于x的方程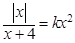 有3个不同的非零的实数解.
有3个不同的非零的实数解.
即方程 有3个不同的非零的实数解,
有3个不同的非零的实数解,
即函数y= 的图象和函数g(x)=
的图象和函数g(x)= 的图象有3个交点,
的图象有3个交点,
画出函数g(x)的图象,如图所示:
故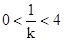 ,
,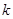 的取值范围是
的取值范围是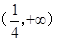 。
。
考点:本题主要考查函数图象,函数方程思想。
点评:中档题,涉及函数方程问题,有时利用数形结合法,通过画出函数图象,往往能形象直观的得出结论。本题关键是能认识到方程 有3个不同的非零的实数解。本题用代数方法讨论,比较繁琐。
有3个不同的非零的实数解。本题用代数方法讨论,比较繁琐。

练习册系列答案
相关题目
设函数 在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是
在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是
| A.f (a+1)= f (2) | B.f (a+1)> f (2) |
| C.f (a+1)< f (2) | D.不确定 |
 ,则
,则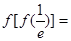 ____________
____________ 的零点为
的零点为 ,则不等式
,则不等式 的最大整数解是 .
的最大整数解是 . 的定义域为___________________
的定义域为___________________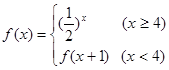 则
则 的值为 .
的值为 .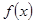 是偶函数,且
是偶函数,且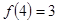 ,那么
,那么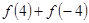 的值为_________
的值为_________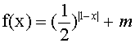 存在有零点,则m的取值范围是__________;
存在有零点,则m的取值范围是__________;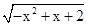 的定义域为______,值域为______.
的定义域为______,值域为______.