题目内容
设函数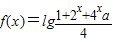 ,a∈R,如果不等式f(x)>(x-1)lg4在区间[1,3]上有解,则实数a的取值范围是 .
,a∈R,如果不等式f(x)>(x-1)lg4在区间[1,3]上有解,则实数a的取值范围是 .
【答案】分析:不等式f(x)>(x-1)lg4化简为1+2x+4xa>4x.将a分离得出a>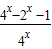 只须a大于g(x)=
只须a大于g(x)=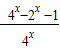 的最小值即可.
的最小值即可.
解答:解: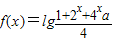 =lg(1+2x+4xa)-lg4.
=lg(1+2x+4xa)-lg4.
等式f(x)>(x-1)lg4即为
lg(1+2x+4xa)>xlg4=lg4x.
1+2x+4xa>4x.
将a分离得出a>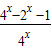
令g(x)=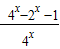
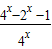 =1-
=1-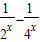 ,只须a大于g(x)的最小值即可
,只须a大于g(x)的最小值即可
易知g(x)在[1,3]上单调递增,最小值为g(1)=1- -
- =
=
所以a>
故答案为:a>
点评:本题考查函数与不等式的综合.参数分离的思想方法.本题得出a大于g(x)=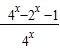 的最小值是关键.
的最小值是关键.
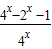 只须a大于g(x)=
只须a大于g(x)=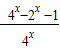 的最小值即可.
的最小值即可.解答:解:
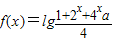 =lg(1+2x+4xa)-lg4.
=lg(1+2x+4xa)-lg4.等式f(x)>(x-1)lg4即为
lg(1+2x+4xa)>xlg4=lg4x.
1+2x+4xa>4x.
将a分离得出a>
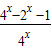
令g(x)=
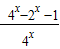
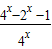 =1-
=1-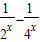 ,只须a大于g(x)的最小值即可
,只须a大于g(x)的最小值即可易知g(x)在[1,3]上单调递增,最小值为g(1)=1-
 -
- =
=
所以a>

故答案为:a>

点评:本题考查函数与不等式的综合.参数分离的思想方法.本题得出a大于g(x)=
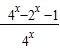 的最小值是关键.
的最小值是关键. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
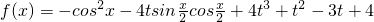 ,x∈R,
,x∈R,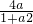 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.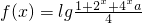 ,a∈R,如果不等式f(x)>(x-1)lg4在区间[1,3]上有解,则实数a的取值范围是________.
,a∈R,如果不等式f(x)>(x-1)lg4在区间[1,3]上有解,则实数a的取值范围是________.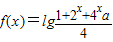 ,a∈R,如果不等式f(x)>(x-1)lg4在区间[1,3]上有解,则实数a的取值范围是 .
,a∈R,如果不等式f(x)>(x-1)lg4在区间[1,3]上有解,则实数a的取值范围是 .