题目内容
设函数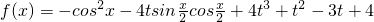 ,x∈R,
,x∈R,
其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤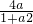 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
解:(1)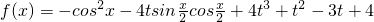 =sin2x-1-2tsinx+4t3+t2-3t+4=sin2x-2tsinx+t2+4t3-3t+3=(sinx-t)2+4t3-3t+3.
=sin2x-1-2tsinx+4t3+t2-3t+4=sin2x-2tsinx+t2+4t3-3t+3=(sinx-t)2+4t3-3t+3.
由(sinx-t)2≥0,|t|≤1,故当sinx=t时,f(x)有最小值g(t),即
g(t)=4t3-3t+3.
(2)我们有g'(t)=12t2-3=3(2t+1)(2t-1),-1<t<1.
列表如下:
| t | (-1,- ) ) | - | (- , , ) ) |  | ( ,1) ,1) |
| g'(t) | + | 0 | - | 0 | + |
| G(t) | ↗ | 极大值g(- ) ) | ↘ | 极小值g( ) ) | ↗ |
由此可见,g(t)在区间(-1,- )和(
)和( ,1)单调增加,在区间(-
,1)单调增加,在区间(- ,
, )单调减小,极小值为g(
)单调减小,极小值为g( )=2,
)=2,
又g(-1)=-4-(-3)+3=2
故g(t)在[-1,1]上的最小值为2
注意到:对任意的实数a,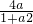 =
=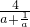 ∈[-2,2]
∈[-2,2]
当且仅当a=1时,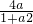 =2,对应的t=-1或
=2,对应的t=-1或 ,
,
故当t=-1或 时,这样的a存在,且a=1,使得g(t)≥
时,这样的a存在,且a=1,使得g(t)≥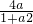 成立.
成立.
而当t∈(-1,1]且t≠ 时,这样的a不存在.
时,这样的a不存在.
分析:(1)利用三角函数转换公式化简f(x),在用配方法得出函数的最简式,即可得出函数g(x)的表达式
(2)求出g(x)的导数,画出表格判断函数的单调性即可求出函数的最值,g(t)≤
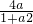 成立,即
成立,即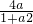 ≥g(t)的最大值,求出a的范围.
≥g(t)的最大值,求出a的范围.点评:该题考查函数的求导,以及利用函数的导数判断函数的单调性进而求出函数的最值,还考查了三角函数的公式的利用,以及恒成立问题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
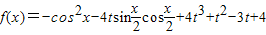 ,x∈R,其中|t|≤1,将f(x)的最小值记为g(t).
,x∈R,其中|t|≤1,将f(x)的最小值记为g(t).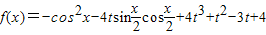 ,x∈R,
,x∈R,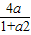 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.