题目内容
(1)在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值.
(2)对5副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.对于下列事件:①A:甲正好取得两只配对手套;②B:乙正好取得两只配对手套.试判断事件A与B是否独立?并证明你的结论.
【答案】
(1) ,或
,或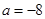 . (2)
. (2) ≠
≠ , A与B是不独立的.
, A与B是不独立的.
【解析】
试题分析: ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: ,即
,即
直线3ρcosθ+4ρsinθ+a=0的普通方程为: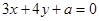 , 4分
, 4分
又圆与直线相切,所以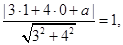
解得: ,或
,或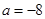 .
7分
.
7分
(2)解:①P(A)=  =
=  ;
;
②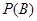 =
= =
=  . 11分
. 11分
∵P(AB)=  =
=  ,
,  =
= , 13分
, 13分
∴ ≠
≠ ,故A与B是不独立的. 15分
,故A与B是不独立的. 15分
考点:本题主要考查极坐标方程与直角坐标方程的互化,直线与圆的位置关系,相互独立事件的概念及其概率计算。
点评:中档题,本题综合性较强,覆盖面较广。考查知识点注重了基础。其中(1)化为直角坐标方程,利用几何法研究直线与圆相切问题,是常见方法。相互独立事件的概率满足 =
= 。
。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目