题目内容
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,则AE,SD所成的角的正弦值为( )
A.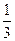 | B.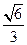 | C.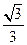 | D.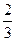 |
B
解析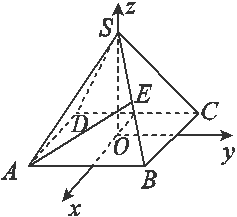
建立如图所示的空间直角坐标系,令四棱锥的棱长为2,
则A(1,-1,0),D(-1,-1,0),S(0,0,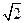 ),
), ,
,
∴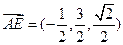 ,
,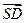 =(-1,-1,
=(-1,-1, ),
),
∴ ,
,
∴AE,SD所成的角的正弦值为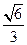 ,选B.
,选B.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
已知正四棱柱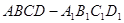 中,
中, ,
,  为
为 的中点,则点
的中点,则点 到平面
到平面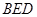 的距离为()
的距离为()
| A.1 | B.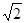 | C. | D.2 |
已知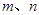 是两条不重合的直线,
是两条不重合的直线, 是三个不重合的平面,则
是三个不重合的平面,则 的一个充分条件是( )
的一个充分条件是( )
A. |
B.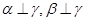 |
C. |
D.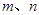 是异面直线, 是异面直线, |
点E,F,G,H分别为空间四边形ABCD中AB,BC,CD,AD的中点,若AC=BD,且AC与 BD所成角的大小为90°,则四边形EFGH是( )
| A.梯形 | B.空间四边形 |
| C.正方形 | D.有一内角为60o的菱形 |
已知α,β表示两个不同的平面,m是一条直线且m?α,则:“α⊥β”是“m⊥β”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
设m,n是两条不同直线,α,β是两个不同的平面,下列命题正确的是( )
| A.m∥α,n∥β且α∥β,则m∥n |
| B.m⊥α,n⊥β且α⊥β,则m⊥n |
| C.m⊥α,n?β,m⊥n,则α⊥β |
| D.m?α,n?α,m∥β,n∥β,则α∥β |
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、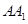 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且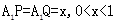 ,设面
,设面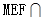 面MPQ=
面MPQ=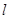 ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )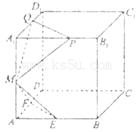
 面ABCD
面ABCD AC
AC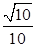
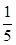
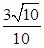
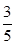
 表示平面,m,n表示直线,
表示平面,m,n表示直线,  ,给出下列四个结论:
,给出下列四个结论: ;②
;②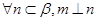 ;③
;③ ;④
;④ ,
,