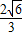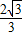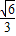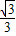题目内容
正三角形ABC边长为2,设
=2
,
=3
,则
•
| BC |
| BD |
| AC |
| AE |
| AD |
| BE |
-2
-2
.分析:由题意可得
=
(
+
),
=
-
,
2 =
2 =4,
•
=2,由此根据
•
=
(
+
)•(
-
),运算求得结果.
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BE |
| 1 |
| 3 |
| AC |
| AB |
| AB |
| AC |
| AC |
| AB |
| AD |
| BE |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AC |
| AB |
解答:解:由题意可得
=
(
+
),
=
-
,
2 =
2 =4,
•
=2×2×cos60°=2.
∴
•
=
(
+
)•(
-
)=
•
•
-
2+
2-
•
=-
•
-
×4+
×4=-2,
故答案为-2.
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BE |
| 1 |
| 3 |
| AC |
| AB |
| AB |
| AC |
| AC |
| AB |
∴
| AD |
| BE |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AC |
| AB |
| 1 |
| 6 |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| 1 |
| 6 |
| AC |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 3 |
| AC |
| AB |
| 1 |
| 2 |
| 1 |
| 6 |
故答案为-2.
点评:本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
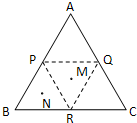 正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是
正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是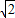 ,则P到平面ABC的距离为( )
,则P到平面ABC的距离为( )