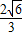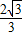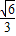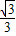题目内容
正三角形ABC边长为2,平面ABC外一点P,PA=PB=PC=
,则P到平面ABC的距离为( )
| 2 |
分析:结合题意画出图形,再过P作底面ABC的垂线,垂足为O,所以得到PO就是P到平面ABC的距离,然后连接CO并延长交AB于E,进而利用解三角形的有关知识求出PO得到答案.
解答: 解:由题意可得:过P作底面ABC的垂线,垂足为O,
解:由题意可得:过P作底面ABC的垂线,垂足为O,
所以PO就是P到平面ABC的距离,
再连接CO并延长交AB于E,
因为P为边长为2的正三角形ABC所在平面外一点且PA=PB=PC=
,
所以O是三角形ABC的中心,并且有CE⊥AB,
所以根据三垂线定理可得:PE⊥AB,
因为正三角形ABC边长为2,
所以CO=
CE=
×
×2=
,
又因为PC=
,
所以PO=
=
.
故选C.
 解:由题意可得:过P作底面ABC的垂线,垂足为O,
解:由题意可得:过P作底面ABC的垂线,垂足为O,所以PO就是P到平面ABC的距离,
再连接CO并延长交AB于E,
因为P为边长为2的正三角形ABC所在平面外一点且PA=PB=PC=
| 2 |
所以O是三角形ABC的中心,并且有CE⊥AB,
所以根据三垂线定理可得:PE⊥AB,
因为正三角形ABC边长为2,
所以CO=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
又因为PC=
| 2 |
所以PO=
2-(
|
| ||
| 3 |
故选C.
点评:解决此类问题的关键是熟练掌握常用几何体的结构特征,本题考查三垂线定理,以及点、线、面间的距离,解决距离问题的关键是根据题意找到所求的线段,考查学生计算能力,逻辑思维能力与空间想象能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
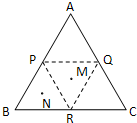 正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是
正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是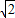 ,则P到平面ABC的距离为( )
,则P到平面ABC的距离为( )