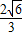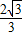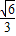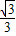题目内容
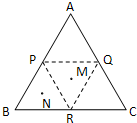正三角形ABC边长为2，P，Q，R，分别是三边的中点，把△APQ，△BPR，△CQR分别沿PQ，PR，QR折起，使得A，B，C重合，M，N分别是△PQR，△BPR的中心，则在几何体中MN的长是| 1 |
| 3 |
| 1 |
| 3 |
分析：由题意知，△PQR、△APQ、△CQR、△PBR均为边长为1的正三角形，由正三角形中心的性质可判断折叠后的图形中，MN∥AQ，且MN=
AQ，由此可得答案．
| 1 |
| 3 |
解答：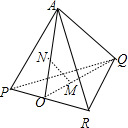
解：由题意知，△PQR、△APQ、△CQR、△PBR均为边长为1的正三角形，
因为M、N分别为△PQR，△BPR的中心，
所以连接BQ必过M、N及PR的中点O，且
=
，
=
，
折叠后图形如右图所示：
则MN∥AQ，且MN=
AQ=
，
故答案为：
．
解：由题意知，△PQR、△APQ、△CQR、△PBR均为边长为1的正三角形，因为M、N分别为△PQR，△BPR的中心，
所以连接BQ必过M、N及PR的中点O，且
| OM |
| OQ |
| 1 |
| 3 |
| ON |
| OA |
| 1 |
| 3 |
折叠后图形如右图所示：
则MN∥AQ，且MN=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查空间中两点间的距离问题，考查学生的空间想象能力，解决本题的关键是充分利用重心的性质．
练习册系列答案
相关题目
，则P到平面ABC的距离为（ ）
