题目内容
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,且椭圆四个顶点构成的菱形面积为
,且椭圆四个顶点构成的菱形面积为![]() .
.
(1)求椭圆C的方程;
(2)若直线l :y=x+m与椭圆C交于M,N两点,以MN为底边作等腰三角形,顶点为P(3,-2),求m的值及△PMN的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据离心率和菱形面积,得到关于![]() 的方程,解出
的方程,解出![]() 得到椭圆方程.
得到椭圆方程.
(2)直线与椭圆联立,利用韦达定理得到![]() ,得到
,得到![]() 中点坐标,然后利用等腰三角形三线合一,即底边中线与底边垂直,构造方程,求出
中点坐标,然后利用等腰三角形三线合一,即底边中线与底边垂直,构造方程,求出![]() 中点坐标,利用弦长公式求出
中点坐标,利用弦长公式求出![]() 的长,利用点
的长,利用点![]() 到直线
到直线![]() 的距离,求出底边
的距离,求出底边![]() 上的高,从而得到
上的高,从而得到![]() 的面积.
的面积.
(1)![]() 椭圆四个顶点构成的菱形面积为
椭圆四个顶点构成的菱形面积为![]()
![]()
![]() 椭圆离心率为
椭圆离心率为![]()
![]()
又![]()
解得![]() ,故所求椭圆C的方程为:
,故所求椭圆C的方程为:![]()
(2)设![]() ,
,![]() ,
,![]() 的中点为
的中点为![]()
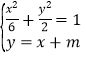 消去
消去![]() 得:
得:![]()
![]()
![]()
![]()
由韦达定理得: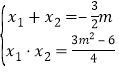
![]() ,
,![]()
所以![]()
![]() 由
由![]()
![]()
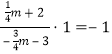 , 解得
, 解得![]() ,满足
,满足![]()
即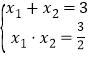
![]()
![]()
顶点![]() 到底边
到底边![]() 的距离为:
的距离为:![]()
所求![]() .
.

练习册系列答案
相关题目