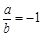题目内容
已知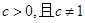 ,设
,设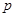 :函数
:函数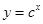 在
在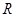 上单调递减;
上单调递减;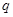 :函数
:函数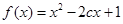 在
在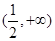 上为增函数.
上为增函数.
(1)若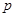 为真,
为真,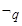 为假,求实数
为假,求实数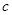 的取值范围;
的取值范围;
(2)若“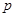 且
且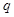 ”为假,“
”为假,“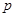 或
或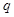 ”为真,求实数
”为真,求实数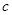 的取值范围.
的取值范围.
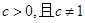 ,设
,设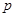 :函数
:函数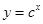 在
在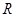 上单调递减;
上单调递减;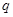 :函数
:函数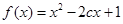 在
在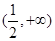 上为增函数.
上为增函数.(1)若
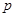 为真,
为真,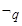 为假,求实数
为假,求实数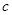 的取值范围;
的取值范围;(2)若“
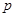 且
且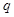 ”为假,“
”为假,“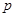 或
或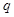 ”为真,求实数
”为真,求实数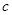 的取值范围.
的取值范围.(1)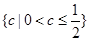 ;(2)
;(2)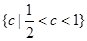 .
.
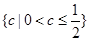 ;(2)
;(2)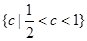 .
.试题分析:先结合指数函数、二次函数的图像与性质得出
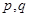 为真时的
为真时的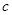 的取值范围,对于(1)只须求出
的取值范围,对于(1)只须求出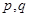 为真时的
为真时的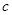 的取值范围的共同部分即可;对于(2)先由题中条件判断出
的取值范围的共同部分即可;对于(2)先由题中条件判断出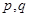 一真一假,从而求出
一真一假,从而求出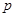 真
真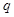 假时的取值范围的共同部分及
假时的取值范围的共同部分及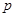 假
假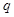 真时的取值范围的共同部分,最后求出这两种情况的并集即可.
真时的取值范围的共同部分,最后求出这两种情况的并集即可.试题解析:
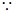 函数
函数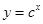 在
在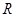 上单调递减,
上单调递减,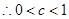 即
即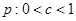 2分
2分函数
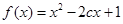 在
在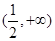 上为增函数,
上为增函数,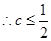 即
即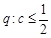 4分
4分(1)
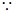
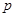 为真,
为真,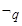 为假
为假由
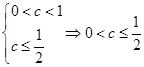
所以实数
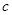 的取值范围是
的取值范围是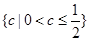 6分
6分(2)又“
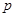 或
或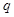 ”为假,“
”为假,“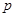 且
且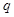 ”为真,
”为真,
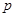 真
真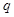 假或
假或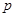 假
假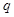 真
真所以由
 或
或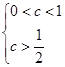 解得
解得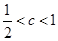
所以实数
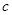 的取值范围是
的取值范围是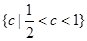 12分.
12分.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
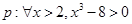 ,那么
,那么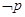 是
是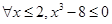
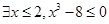
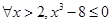
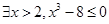
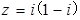 ,
, 在复平面内对应的点位于第四象限;
在复平面内对应的点位于第四象限;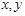 是实数,则“
是实数,则“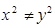 ”的充要条件是“
”的充要条件是“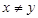 或
或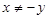 ”;
”;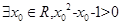 ”的否定
”的否定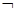 P:“
P:“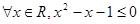 ”;
”;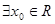 ,
,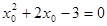 的否定形式为 .
的否定形式为 .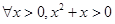 ”的否定是 .
”的否定是 .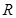 的函数
的函数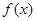 不是奇函数,则下列命题中一定为真命题的是( )
不是奇函数,则下列命题中一定为真命题的是( )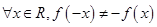
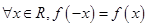
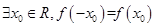
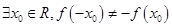
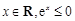
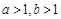 是
是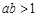 的充分条件
的充分条件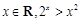
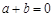 的充要条件是
的充要条件是