题目内容
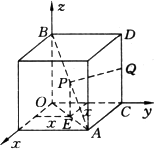
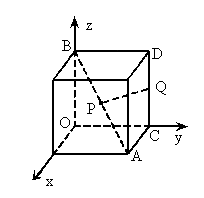
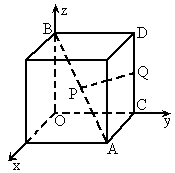
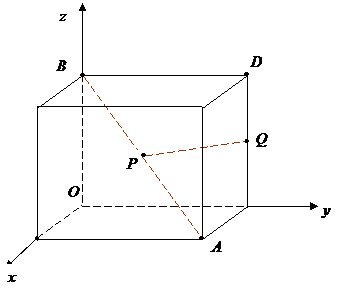
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O-xyz,点P在对角线AB上运动,点Q为棱CD的中点,探求|PQ|的最小值.
答案:
解析:
提示:
解析:
解:如图,过P作PE⊥OA于E,则PE⊥面xOy,设点P的x坐标为x,由正方体性质得点P的y坐标为x,取正方体棱长为1,则![]() .
.
提示:
分析:根据正方形的性质设出P、Q的坐标,由两点距离公式建立|PQ|的表达式,利用函数求最值的方法求解.
解题心得:事实上,当P、Q分别为AB、CD中点时,可证明PQ为异面直线AB、CD的公垂线,由此可知异面直线上任意两点之间以公垂线段为最短.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
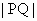 的最小值;
的最小值;
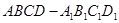 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系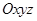 ,
,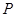 在线段
在线段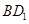 上,且满足
上,且满足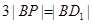 ,试写出点
,试写出点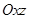 的对称点
的对称点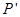 的坐标;
的坐标;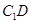 中点为
中点为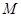 ,求点
,求点