题目内容
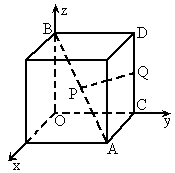
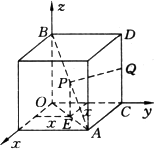
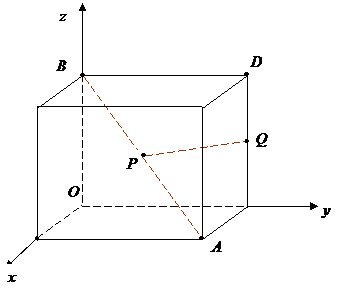
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.
(1)当点P为对角线AB的中点,点在Q在棱CD上运动时,探究|PQ|的最小值;
(2)当点Q为棱CD的中点,点P在对角线上运动时,探究|PQ|的最小值.
答案:略
解析:
解析:
|
解:设正方体棱长为 2a,则A(2a,2a,0),B(0,0,2a),C(0,2a,0)D(0 ,2a,2a),O(0,0,0),(1) ∵P为AB的中点,∴设P点坐标为(a,a,a)又 Q点在CD上运动,∴设Q点坐标为(0,2a,z)∴ 
当且仅当 a=z时,|PQ|最小,最小值为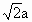 ,此时,P、Q在平行于xOy平面的平面上. ,此时,P、Q在平行于xOy平面的平面上.
(2) 连结BQ、QA,则△AQB为等腰三角形,∴|PQ|的最小值为过Q作BA的垂线段的长,即P为AB中点,其最小值为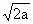 . . |

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
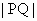 的最小值;
的最小值;
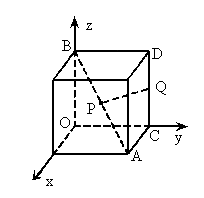
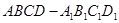 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系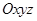 ,
,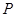 在线段
在线段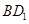 上,且满足
上,且满足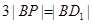 ,试写出点
,试写出点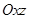 的对称点
的对称点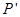 的坐标;
的坐标;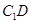 中点为
中点为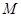 ,求点
,求点