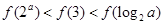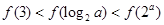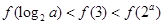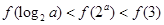题目内容
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
C
解析试题分析: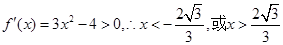 ,即函数在
,即函数在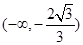 和
和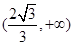 上单调递增,在区间
上单调递增,在区间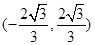 上单调递减,
上单调递减,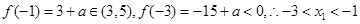 ,所以A错误;
,所以A错误;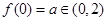 ,所以当
,所以当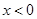 时,只有一个零点,所以
时,只有一个零点,所以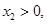 所以C正确.
所以C正确.
考点:本小题主要考查利用导数判断函数的单调性和利用零点存在定理判断函数的零点范围.
点评:当函数的零点不易求出时,可以根据零点存在定理判断零点的取值范围。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
若 有极大值和极小值,则
有极大值和极小值,则 的取值范围是 ( )
的取值范围是 ( )
A.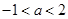 | B.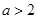 或 或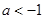 | C.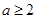 或 或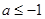 | D. 或 或 |
下列图像中有一个是函数
 的导数
的导数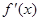 的图像,则
的图像,则 ( )
( )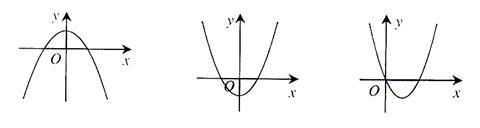
A. | B. | C.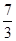 | D. 或 或 |
一个物体的运动方程为 其中
其中 的单位是米,
的单位是米,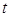 的单位是秒,那么物体在
的单位是秒,那么物体在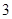 秒末的瞬时速度是( )
秒末的瞬时速度是( )
A. 米/秒 米/秒 | B. 米/秒 米/秒 | C. 米/秒 米/秒 | D. 米/秒 米/秒 |
函数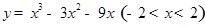 有( )
有( )
| A.极大值5,极小值 27 | B.极大值5,极小值 11 |
| C.极大值5,无极小值 | D.极小值 27,无极大值 |
函数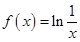 ,则此函数图像在点
,则此函数图像在点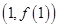 处的切线的倾斜角为 ( )
处的切线的倾斜角为 ( )
| A.0 | B. | C.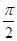 | D.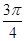 |
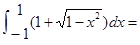 ( )
( )
A.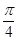 | B.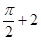 | C.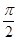 | D.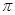 |
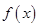 在D上可导,即
在D上可导,即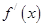 存在,且导函数
存在,且导函数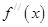 =
=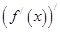 ,若
,若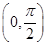 上不是凸函数的是( )
上不是凸函数的是( ) 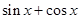
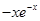
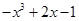

 对定义域
对定义域 内的任意
内的任意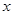 都有
都有
 ,且当
,且当 时,其导函数
时,其导函数 满足
满足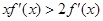 ,若
,若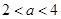 ,则有
,则有