题目内容
身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
| A.24种 | B. 28种 | C.36种 | D. 48种 |
D
解析试题分析:由题意知先使五个人的全排列,共有A55种结果,去掉相同颜色衣服的人都相邻的情况,再去掉仅穿蓝色衣服的人的相邻和仅穿穿黄色衣服的人相邻两种情况,从而求得结果.
由题意知先使五个人的全排列,共有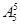 种结果.
种结果.
去掉同颜色衣服相的人都相邻的情况,再去掉仅穿蓝色相邻和仅穿黄色相邻的两种情况.
穿相同颜色衣服的人都相邻的情况有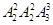 种(相邻的看成一整体),
种(相邻的看成一整体),
当穿兰色衣服的相邻,而穿黄色衣服的人不相邻,共有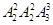 种(相邻的看成一整体,不相邻利用插空法),同理当穿黄色衣服的相邻,而穿兰色衣服的人不相邻,也共有
种(相邻的看成一整体,不相邻利用插空法),同理当穿黄色衣服的相邻,而穿兰色衣服的人不相邻,也共有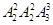 种,
种,
∴穿相同颜色衣服的人不能相邻的排法是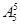 -
-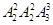 -2
-2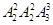 =48,
=48,
故答案 D
考点:排列组合的运用
点评:本题是一个简单计数问题,在解题时注意应用排除法,从正面来解题时情况比较复杂,所以可以写出所有的结果,再把不合题意的去掉.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有 ( )
| A.96种 | B.180种 | C.240种 | D.280种 |
方程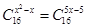 的解共有( )
的解共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )
| A.60种 | B.63种 | C.65种 | D.66种 |
已知二项式 的展开式中第4项为常数项,则
的展开式中第4项为常数项,则 项的系数为( )
项的系数为( )
| A.-19 | B.19 | C.20 | D.-20 |
甲、乙两人计划从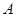 、
、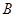 、
、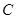 三个景点中各选择两个游玩,则两人所选景点不全相同的选法共有( )
三个景点中各选择两个游玩,则两人所选景点不全相同的选法共有( )
| A.3种 | B.6种 | C.9种 | D.12种 |
若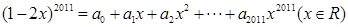 ,则
,则 ( )
( )
| A.2009 | B.2010 | C.2011 | D.2012 |
从0,1,2,3,4,5,6,7,8,9这10个数字中任取3个不同的数字构成空间直角坐标系中的点的坐标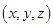 ,若
,若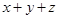 是3的倍数,则满足条件的点的个数为
是3的倍数,则满足条件的点的个数为
| A.252 | B.216 | C.72 | D.42 |
从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有( )
| A.140种 | B.120种 | C.35种 | D.34种 |