题目内容
若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )
| A.60种 | B.63种 | C.65种 | D.66种 |
D
解析试题分析:由题意知本题是一个分类计数问题,要得到四个数字的和是偶数,需要分成三种不同的情况,
当取得4个偶数时,有 =1种结果,
=1种结果,
当取得4个奇数时,有 =5种结果,
=5种结果,
当取得2奇2偶时有 =6×10=60
=6×10=60
∴共有1+5+60=66种结果,故选D.
考点:本题主要考查分类计数原理,简单的排列组合问题。
点评:简单题,简单的排列组合问题,一般的可直接分类分步、套用公式,有附加条件的,往往从特殊元素、特殊位置入手。

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
旅游公司为3个旅游团提供4条旅游线路,每个旅游团只能任选其中一条,则不同的选择方法有( )种.
| A.24 | B.48 | C.64 | D.81 |
在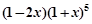 的展开式中,
的展开式中,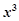 的系数是
的系数是
| A.20 | B.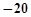 | C.10 | D.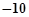 |
由 ,
, ,
, ,
, 组成没有重复数字的三位数,其中奇数的个数为( )
组成没有重复数字的三位数,其中奇数的个数为( )
| A.36 | B.24 | C.12 | D.6 |
如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法共有( )
| A.264种 | B.288种 | C.240种 | D.168种 |
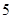 个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有( )
个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有( )
A.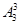 | B.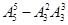 | C.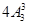 | D.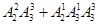 |
身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
| A.24种 | B. 28种 | C.36种 | D. 48种 |
设 展开后为1+
展开后为1+
 +
+
 +……+
+……+
 ,
, +
+ =
=
| A.20 | B.200 | C.55 | D.180 |
n∈N*,则(20-n)(21-n)……(100-n)等于( )
A.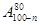 | B.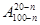 |
C.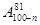 | D.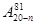 |