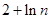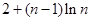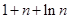题目内容
已知数列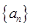 的前n项和
的前n项和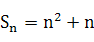 ,在各项为正数的数列
,在各项为正数的数列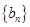 中
中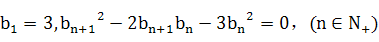
(1)求数列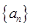 和
和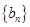 的通项公式;
的通项公式;
(2)令Cn=an.bn求数列{Cn}的前n项和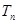
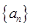 的前n项和
的前n项和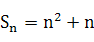 ,在各项为正数的数列
,在各项为正数的数列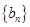 中
中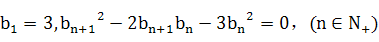
(1)求数列
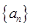 和
和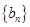 的通项公式;
的通项公式;(2)令Cn=an.bn求数列{Cn}的前n项和
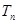
(1) 
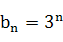
(2) ∴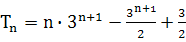

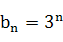
(2) ∴
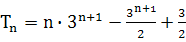
(1)先根据条件得到数列项的递推式,再利用定义求出数列的通项公式;(2)根据数列特征,利用错位相减的思想求出数列的前n项和
(1) 当n=1时,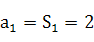 ; 当
; 当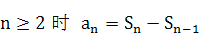
 =2n检验当n=1时
=2n检验当n=1时 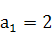 ,
,
因为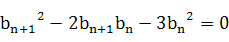
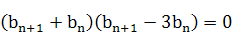
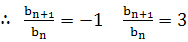
因为 ,
,
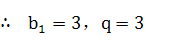 所以
所以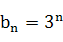

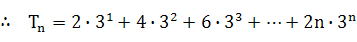
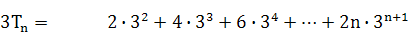
两式相减得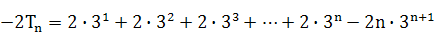
∴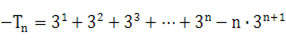 ∴
∴
∴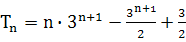
(1) 当n=1时,
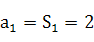 ; 当
; 当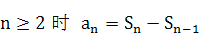
 =2n检验当n=1时
=2n检验当n=1时 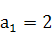 ,
,
因为
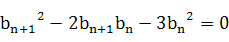
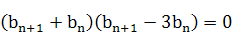
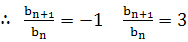
因为
 ,
,
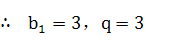 所以
所以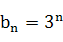

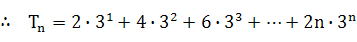
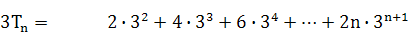
两式相减得
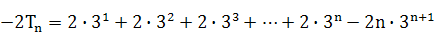
∴
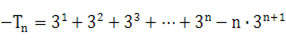 ∴
∴
∴
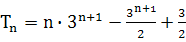

练习册系列答案
相关题目
 的前n项和
的前n项和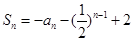 (n为正整数)。
(n为正整数)。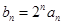 ,求证数列
,求证数列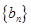 是等差数列,
是等差数列,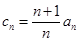 ,
,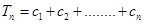 。是否存在最小的正整数
。是否存在最小的正整数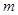 ,使得对于
,使得对于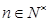 都有
都有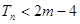 恒成立,若存在,求出
恒成立,若存在,求出 的前n项和为
的前n项和为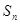 ,
,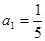 ,向量
,向量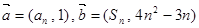 ,其中
,其中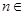 N*,且
N*,且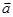 ∥
∥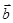 .
.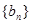 的前n项和为
的前n项和为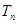 ,且
,且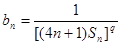 (其中
(其中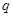 是首项
是首项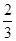 ,第四项为
,第四项为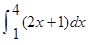 的等比数列的公比),求证:
的等比数列的公比),求证: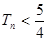 .
.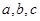 ,且A,B,C成等差数列,
,且A,B,C成等差数列,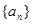 的通项公式是
的通项公式是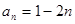 ,其前
,其前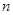 项和为
项和为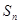 ,则数列
,则数列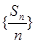 的前11项和为( )
的前11项和为( )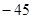
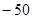
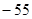
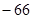
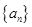 中,已知
中,已知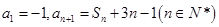 。
。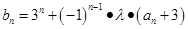 (
(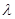 为非零常数),问是否存在整数
为非零常数),问是否存在整数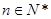 都有
都有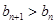 ?若存在,求出
?若存在,求出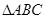 中角
中角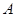 、
、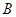 、
、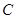 成等差数列,则
成等差数列,则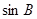 =( )
=( )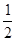
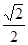
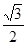
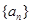 中,
中,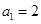 ,
, 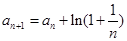 ,则
,则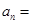 ( )
( )