题目内容

9．复数z使|z|=1成立，求|z+1-2i|的最大值和最小值及相应的z．

分析 满足|z|=1的复数z，在以原点为圆心，以1为半径的圆上，|z+1-2i|表示复数z在复平面内对应点Z到点A（-1，2）的距离，即可求解|z+1-2i|的最值．通过直线与圆的方程求解z即可．

解答 解：满足|z|=1的复数z，在以原点为圆心，以1为半径的圆上． 而|z+1-2i|表示复数z在复平面内对应点Z到点A（-1，2）
的距离，OA=$\sqrt{5}$，|z+1-2i|的最小值是 $\sqrt{5}-1$，
|z+1-2i|的最大值为$\sqrt{5}+1$．由OA的方程为：y=-2x，|z|=1表示x2+y2=1，联立可得x=±$\frac{\sqrt{5}}{5}$，
|z+1-2i|的最小值是 $\sqrt{5}-1$时，z=$-\frac{\sqrt{5}}{5}$+$\frac{2\sqrt{5}}{5}i$．
|z+1-2i|的最大值为$\sqrt{5}+1$时，z=$\frac{\sqrt{5}}{5}-\frac{2\sqrt{5}}{5}i$．

点评 本题考查两个复数差的模的几何意义，复数的应用，是一道中档题．

练习册系列答案
相关题目
19．已知函数f（x）=$\left\{\begin{array}{l}2-（\frac{1}{2}）^{x}，&x≤0\\ 2{x}^{2}+1，&x＞0\end{array}\right.$，g（x）=kx，若函数h（x）=f（x）-g（x）有3个不同的零点，则实数k的取值范围是（　　）
A．（-∞，0）B．[2$\sqrt{2}$，+∞）C．（0，+∞）D．（2$\sqrt{2}$，+∞）
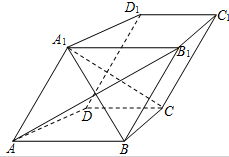20．已知菱形ABCD的边长为2，∠BAD=120°，点E、F分别在边BC、DC上，$\overrightarrow{BE}$=λ$\overrightarrow{BC}$，$\overrightarrow{DF}$=μ$\overrightarrow{DC}$．若$\overrightarrow{AE}•\overrightarrow{AF}$=1，$\overrightarrow{CE}$•$\overrightarrow{CF}$=-$\frac{2}{3}$，则λ+μ=$\frac{5}{6}$．
17．如图，在四棱柱ABCD-A1B1C1D1中，AB∥CD，AB1⊥BC，且AA1=AB．
（1）求证：AB∥平面D1DCC1；
（2）求证：AB1⊥平面A1BC．
4．判断下列问题是否是排列问题：
（1）从7名同学中选派3人去完成3种不同的工作，每人完成一种，有多少种不同的选派方法；
（2）从7名同学中选3人去某地参加一个会议，有多少种不同的选派方法？
14．已知数列{an}中，a1=-60，an+1=an+3，求数列{|an|}的前n项和．
1．设数列{an}的前n项和为Sn，对任意的正整数n，都有Sn=2an+n-3成立．
（1）求证：数列{an-1}为等比数列；
（2）求数列{nan}的前n项和Tn．
18．设函数f（x）=x2-ax+lnx（a为常数）．
（Ⅰ）当a=3时，求函数f（x）的极值；
（Ⅱ）当0＜a＜2$\sqrt{2}$时，试判断f（x）的单调性；
（Ⅲ）对任意x0∈[1，2]，使不等式f（x0）＜mlna对任意a∈（0，$\frac{1}{2}$）恒成立，求实数m的取值范围．
19．设M是焦距为2的椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上一点，A，B是其左右顶点，直线MA与MB的斜率分别为k1，k2，且k1k2=-$\frac{1}{2}$．
（1）求椭圆E的方程；
（2）已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上点N（x0，y0）处切线方程为$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1，若与与椭圆E相切与（x1，y1），D（x2，y2）两点的切线相交于P点，且$\overrightarrow{PC}$•$\overrightarrow{PD}$=0，求证点P到原点距离为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网