题目内容

17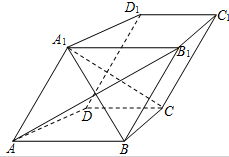．如图，在四棱柱ABCD-A1B1C1D1中，AB∥CD，AB1⊥BC，且AA1=AB．
（1）求证：AB∥平面D1DCC1；
（2）求证：AB1⊥平面A1BC．

分析 （1）由AB∥CD，且CD?平面D1DCC1，AB?平面D1DCC1，由线面平行的判定定理即可证明AB∥平面D1DCC1；
（2）证明AB1⊥平面A1BC，只需证明AB1⊥A1B，利用四边形ABB1A1为菱形即可；

解答 证明：（1）∵AB∥CD，CD?平面D1DCC1，AB?平面D1DCC1；
∴AB∥平面D1DCC1；…（3分）
（2）在四棱柱ABCD-A1B1C1D1中，四边形ABB1A1为平行四边形，
∵AA1=AB，
∴四边形ABB1A1为菱形，
∴AB1⊥A1B，
∵AB1⊥BC，A1B∩BC=B，
∴AB1⊥平面A1BC，…（8分）

点评 本题考查线面垂直的证明，直线与平面平行的判定，考查学生分析解决问题的能力，考查了空间想象能力和转化思想，属于基本知识的考查．

练习册系列答案
相关题目
7．已知抛物线的顶点在坐标原点，对称轴是y轴，经过点A（2，1），M（x1，y1），N（x2，y2）是抛物线上异于点A的两点，∠MAN=$\frac{π}{2}$．
（1）求抛物线的方程；
（2）求证：直线MN经过定点，并求定点坐标；
（3）若x2＜2＜x1，点M，A，N在x轴上的投影分别是R，S，T，求$\frac{|TS|}{|SR|}$的最小值．
8．作图验证：
（1）$\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）+\frac{1}{2}（\overrightarrow{a}-\overrightarrow{b}）=\overrightarrow{a}$
（2）$\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）-\frac{1}{2}（\overrightarrow{a}-\overrightarrow{b}）=\overrightarrow{b}$．
5．对?a，b∈R，记min{a，b}=$\left\{\begin{array}{l}{a，（a＜b）}\\{b（a≥b）}\end{array}\right.$，则函数f（x）=min{|x+1|，|x-1|}（x∈R）的单调增区间为（　　）
A．[0，+∞）B．（-∞，0]C．（-∞，-1]和[0，1]D．[-1，0]和[1，+∞）
12．在一台小型的晚会上有歌曲、戏曲、魔术、小品、相声、舞蹈、杂技7个表演节目，其中歌曲节目必须放在最后，且魔术节目不能和相声节目相邻，也不能和小品节目相邻，则不同的表演顺序的种数为（　　）
A．216B．72C．144D．288
2．若关于x的不等式x2+ax-c＜0的解集为{x|-2＜x＜1}，且函数y=ax3+mx2+x+$\frac{c}{2}$在区间（$\frac{1}{2}$，1）上不是单调函数，则实数m的取值范围是（　　）
A．（-2，-$\sqrt{3}$）B．（-∞，-2）∪（$\sqrt{3}$，+∞）C．[-3，-$\sqrt{3}$]D．（-∞，-2）∪（-$\sqrt{3}$，+∞）
9．复数z使|z|=1成立，求|z+1-2i|的最大值和最小值及相应的z．
6．求下列函数的导数．
（1）y=esin（ax+b）；
（2）y=xloga（x2+x-1）．
7．已知偶函数f（x）满足f（x+2）=f（x），且当x∈[0，1]时，f（x）=x．若在区间[-1，3]上，函数g（x）=f（x）-kx-k有3个零点，则实数k的取值范围是（$\frac{1}{4}$，$\frac{1}{2}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网