题目内容

如图，已知长方体ABCD－A1B1C1D1中，E、F为棱AD．AB的中点．A1C1和B1D1相交于点O．A1C1＝2a，BB1＝B1C1＝a，

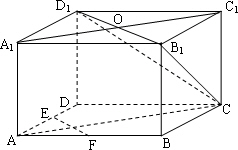
(Ⅰ)求证：EF∥平面CB1D1；

(Ⅱ)求直线B1C与平面ACC1A1所成角的正弦值．

答案：
解析：

　　证明：(Ⅰ)连结BD．在长方体AC1中，对角线BD‖B1D1．

　　又∵E、F为棱AD．AB的中点，

　　∴

　　∴　3分

　　又∵B1D1平面，平面，

　　∴EF∥平面CB1D1．　6分

　　(Ⅱ)∵在长方体中，AA1⊥平面A1B1C1D1，而AA1平面AC·C1A1，

　　∴平面ACC1A1⊥平面A1B1C1D1，且平面ACC1A1∩平面A1B1C1D1＝A1C1

　　∵在RT⊿A1B1C1中，A1C1＝2a＝2B1C1，易知，⊿OB1C1是等边三角形．　8分

　　取OC1中点M，连结B1M，则有B1M⊥A1C1，∴B1M⊥平面ACC1A1

　　连结MC，则∠B1CM即为直线B1C与平面ACC1A1所成角　10分

　　在RT⊿B1MC中，B1M＝，B1C＝

　　∴sin∠B1CM＝　12分


练习册系列答案
相关题目
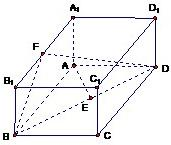
精英家教网如图，已知长方体ABCD-A1B1C1D1，AB=2，AA1=1，直线BD与平面AA1B1B所成的角为30°，AE垂直BD于E，F为A1B1的中点．
（I）求异面直线AE与BF所成的角；
（II）求平面BDF与平面AA1B所成二面角（锐角）的大小
（III）求点A到平面BDF的距离．
如图，已知长方体ABCD-A1B1C1D1中，AB=2
3
，AD=2
3
，AA1=2．
求：
①BC和A1C1所成的角度是多少度？
②AA1和B1C1所成的角是多少度？
如图，已知长方体ABCD-A1B1C1D1中，AB=3，AD=AA1=2，点O是线段BC1的中点，点M是OD的中点，点E是线段AB上一点，AE＞BE，且A1E⊥OE．
①求AE的长；
②求二面角A1-DE-C的正切值；
③求三棱锥M-A1OE的体积．
如图，已知长方体ABCD-A′B′C′D′中，AB=2
3
，AD=2
3
，AA′=2，
（1）哪些棱所在直线与直线BA’是异面直线？
（2）直线BC与直线A’C’所成角是多少度？
（3）哪些棱所在直线与直线AA’是垂直？
（2008•宣武区一模）如图，已知长方体AC1中，AB=BC=1，BB1=2，连接B1C，过B点作B1C的垂线交CC1于E，交B1C于F
（1）求证：AC1⊥平面EBD；
（2）求点A到平面A1B1C的距离；
（3）求直线DE与平面A1B1C所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网