题目内容
 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.①求AE的长;
②求二面角A1-DE-C的正切值;
③求三棱锥M-A1OE的体积.
分析:①以DA,DC,DD1为x,y,z轴建立空间直角坐标系,设AE=m(1,5<m<3),确定
、
的坐标,利用A1E⊥OE,即可求得结论;
②过点A作AH⊥DE,垂足为H,连接A1H,则∠A1HA是二面角A1-DE-A的平面角,由此可求二面角A1-DE-C的正切值;
③点M是OD的中点,O∈B1C,且B1C∥A1D,利用等体积,可求三棱锥M-A1OE的体积.
| A1E |
| EO |
②过点A作AH⊥DE,垂足为H,连接A1H,则∠A1HA是二面角A1-DE-A的平面角,由此可求二面角A1-DE-C的正切值;
③点M是OD的中点,O∈B1C,且B1C∥A1D,利用等体积,可求三棱锥M-A1OE的体积.
解答: 解:①以DA,DC,DD1为x,y,z轴建立空间直角坐标系,
解:①以DA,DC,DD1为x,y,z轴建立空间直角坐标系,
设AE=m(1,5<m<3),则A1(2,0,2),E(2,m,0),O(1,3,1)
∴
=(0,m,-2),
=(-1,3-m,1)
∵A1E⊥OE
∴m(3-m)-2=0
∴m2-3m+2=0
∴m=2,即AE=2;
②过点A作AH⊥DE,垂足为H,连接A1H,则
∵A1A⊥平面ABCD
∴A1H⊥DE
∴∠A1HA是二面角A1-DE-A的平面角
∵AD=AE=2,∴AH=
∴tan∠A1HA=
∵二面角A1-DE-C是钝角
∴二面角A1-DE-C的正切值为-
;
③∵点M是OD的中点,O∈B1C,且B1C∥A1D,
∴VM-A1OE=
VD-A1OE=
VO-A1DE=
VC-A1DE=
VA1-CDE=
×
×
×3×2×2=1
 解:①以DA,DC,DD1为x,y,z轴建立空间直角坐标系,
解:①以DA,DC,DD1为x,y,z轴建立空间直角坐标系,设AE=m(1,5<m<3),则A1(2,0,2),E(2,m,0),O(1,3,1)
∴
| A1E |
| EO |
∵A1E⊥OE
∴m(3-m)-2=0
∴m2-3m+2=0
∴m=2,即AE=2;
②过点A作AH⊥DE,垂足为H,连接A1H,则
∵A1A⊥平面ABCD
∴A1H⊥DE
∴∠A1HA是二面角A1-DE-A的平面角
∵AD=AE=2,∴AH=
| 2 |
∴tan∠A1HA=
| 2 |
∵二面角A1-DE-C是钝角
∴二面角A1-DE-C的正切值为-
| 2 |
③∵点M是OD的中点,O∈B1C,且B1C∥A1D,
∴VM-A1OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查面面角,考查三棱锥体积的计算,考查空间向量知识的运用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
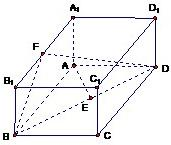 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点. 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB= 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F