题目内容
 如图,已知长方体ABCD-A1B1C1D1中,AB=2
如图,已知长方体ABCD-A1B1C1D1中,AB=2| 3 |
| 3 |
求:
①BC和A1C1所成的角度是多少度?
②AA1和B1C1所成的角是多少度?
分析::①长方体ABCD-A1B1C1D1中,由A1C1∥AC,知∠BCA是BC和A1C1所成的角,由此能求出BC和A1C1所成的角.
②由AA1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,能求出AA1和B1C1所成的角.
②由AA1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,能求出AA1和B1C1所成的角.
解答:解:①长方体ABCD-A1B1C1D1中,
∵AB=2
,AD=2
,AA1=2,
∴AC=
=2
,
∵A1C1∥AC,
∴∠BCA是BC和A1C1所成的角,
∵cos∠BCA=
=
,
∴∠BAC=45°,故BC和A1C1所成的角度是45°.
②∵AA1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,
∴AA1⊥B1C1,
∴AA1和B1C1所成的角是90°.
∵AB=2
| 3 |
| 3 |
∴AC=
(2
|
| 6 |
∵A1C1∥AC,
∴∠BCA是BC和A1C1所成的角,
∵cos∠BCA=
(2
| ||||||
2×2
|
| ||
| 2 |
∴∠BAC=45°,故BC和A1C1所成的角度是45°.
②∵AA1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,
∴AA1⊥B1C1,
∴AA1和B1C1所成的角是90°.
点评:本题考查异面直线所成角的大小的求法,是基础题.解题要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
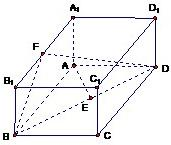 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点. 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE. 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F