题目内容
 已知一个三棱锥的三视图如图所示,其中主视图、俯视图是全等的等腰直角三角形,则该三棱锥的外接球体积为
已知一个三棱锥的三视图如图所示,其中主视图、俯视图是全等的等腰直角三角形,则该三棱锥的外接球体积为36π
36π
.分析:将三视图还原,得它是三棱锥A-BCD,其中△ACD和△BCD是全等的等腰直角三角形,且所在平面互相垂直.由此易得三棱锥外接球心是△ACD和△BCD公共斜边CD的中点E,得球半径R=3,再结合球的体积公式,即可得到该三棱锥的外接球体积.
解答:解: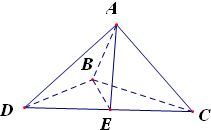 将三视图还原,可得它的实物如右图的三棱锥A-BCD
将三视图还原,可得它的实物如右图的三棱锥A-BCD
其中平面ACD⊥平面BCD,△ACD≌△BCD,且它们都是等腰直角三角形
E为CD的中点,连接AE、BE,得△AEB是等腰直角三角形
由此可得:EA=EB=EC=ED=3
∴点E是三棱锥A-BCD的外接球的球心,得外接球半径R=3
因此,得该三棱锥的外接球体积为V=
×R3=
×33=36π
故答案为:36π
 将三视图还原,可得它的实物如右图的三棱锥A-BCD
将三视图还原,可得它的实物如右图的三棱锥A-BCD其中平面ACD⊥平面BCD,△ACD≌△BCD,且它们都是等腰直角三角形
E为CD的中点,连接AE、BE,得△AEB是等腰直角三角形
由此可得:EA=EB=EC=ED=3
∴点E是三棱锥A-BCD的外接球的球心,得外接球半径R=3
因此,得该三棱锥的外接球体积为V=
| 4π |
| 3 |
| 4π |
| 3 |
故答案为:36π
点评:本题将三视图还原为实物,并且求外接球的体积,着重考查了三视图的认识与理解和球内接多面体等知识,属于基础题.

练习册系列答案
相关题目
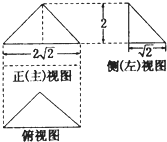 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为( )
已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为( )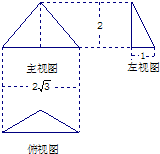 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为 (2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )
(2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )