题目内容
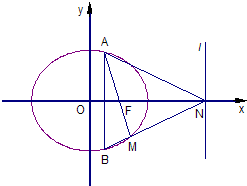 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
分析:(I)根据题意,可得a=2且c=1,利用平方关系算出b2=3,因此可求出椭圆C的方程;
(II)(ⅰ)根据题意,得F(1,0),N(4,0).设A(m,n),则B(m,-n),可得AF、BN以m、n为参数的方程,联解得出M(
,
),再M坐标代入椭圆方程加以验证,即可得到点M恒在椭圆C上;
(ii)设AM的方程为x=ty+1,与椭圆方程消去x得(3t2+4)y2+6ty-9=0.设A(x1,y1),M(x2,y2),由韦达定理将y1+y2、y1y2表示为关于t的式子,从而可得|y1-y2|=
,然后换元:令3t2+4=λ (λ≥4),可得|y1-y2=4
•
,根据二次函数的性质算出当
=
时即t=0时,|y1-y2|取得最大值3,由此可得△AMN面积的最大值为
.
(II)(ⅰ)根据题意,得F(1,0),N(4,0).设A(m,n),则B(m,-n),可得AF、BN以m、n为参数的方程,联解得出M(
| 5m-8 |
| 2m-5 |
| 3n |
| 2m-5 |
(ii)设AM的方程为x=ty+1,与椭圆方程消去x得(3t2+4)y2+6ty-9=0.设A(x1,y1),M(x2,y2),由韦达定理将y1+y2、y1y2表示为关于t的式子,从而可得|y1-y2|=
4
| ||||
| 3t2+4 |
| 3 |
-(
|
| 1 |
| λ |
| 1 |
| 4 |
| 9 |
| 2 |
解答:解:(I)由题意得a=2且c=1
∴为
+
=1
(II)(ⅰ)根据题意,得F(1,0),N(4,0)
设A(m,n),则B(m,-n) (n≠0)
可得
+
=1
∵AF、BN方程分别为m(x-1)-(m-1)y=0
和m(x-4)-(m-4)y=0
∴M(x0,y0)满足
,
联解得x0=
,y0=
由于
+
=
(
)2+
(
)2=
=
=1
所以点M恒在椭圆C上;
(ii)设AM的方程为x=ty+1,与
+
=1消去x得(3t2+4)y2+6ty-9=0
设A(x1,y1),M(x2,y2),可得y1+y2=
,y1y2=
∴|y1-y2|2=(y1+y2)2-4y1y2=(
)2+
=
可得|y1-y2|=
=
令3t2+4=λ (λ≥4),可得|y1-y2|=4
•
=4
•
∵λ≥4,可得
∈(0,
],
∴当
=
时,即t=0时,|y1-y2|取得最大值3,此时AM经过点F
∵△AMN面积S=
|FN|•|y1-y2|=
|y1-y2|≤
∴当t=0时,即直线AB与x轴垂直时,△AMN面积的最大值为
.

∴为
| x2 |
| 4 |
| y2 |
| 3 |
(II)(ⅰ)根据题意,得F(1,0),N(4,0)
设A(m,n),则B(m,-n) (n≠0)
可得
| m2 |
| 4 |
| n2 |
| 3 |
∵AF、BN方程分别为m(x-1)-(m-1)y=0
和m(x-4)-(m-4)y=0
∴M(x0,y0)满足
|
联解得x0=
| 5m-8 |
| 2m-5 |
| 3n |
| 2m-5 |
由于
| x02 |
| 4 |
| y02 |
| 3 |
| 1 |
| 4 |
| 5m-8 |
| 2m-5 |
| 1 |
| 3 |
| 3n |
| 2m-5 |
| (5m-8)2+12n2 |
| 4(2m-5)2 |
| (5m-8)2+36-9m 2 |
| 4(2m-5)2 |
所以点M恒在椭圆C上;
(ii)设AM的方程为x=ty+1,与
| x2 |
| 4 |
| y2 |
| 3 |
设A(x1,y1),M(x2,y2),可得y1+y2=
| -6t |
| 3t2+4 |
| -9 |
| 3t2+4 |
∴|y1-y2|2=(y1+y2)2-4y1y2=(
| -6t |
| 3t2+4 |
| 36 |
| 3t2+4 |
| 144t2+144 |
| (3t2+4)2 |
可得|y1-y2|=
|
4
| ||||
| 3t2+4 |
令3t2+4=λ (λ≥4),可得|y1-y2|=4
| 3 |
-
|
| 3 |
-(
|
∵λ≥4,可得
| 1 |
| λ |
| 1 |
| 4 |
∴当
| 1 |
| λ |
| 1 |
| 4 |
∵△AMN面积S=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
∴当t=0时,即直线AB与x轴垂直时,△AMN面积的最大值为
| 9 |
| 2 |
点评:本题给出椭圆满足的条件,求椭圆的方程,并求证直线经过定点、求△AMN面积的最大值.着重考查了椭圆的标准方程与简单几何性质、直线与圆锥曲线位置关系等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
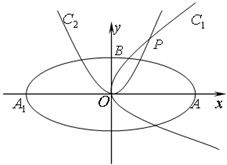 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 如图,椭圆
如图,椭圆 如图,椭圆
如图,椭圆 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: