Question

如图，△ABC是某屋顶的断面，CD⊥AB，横梁AB的长是竖梁CD长的2倍.设计时，应使y=tanA+2tanB保持最小，试确定D点位置，并求y的最小值.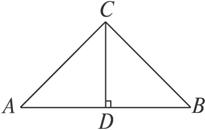

Answer 1

解：设AD=x,CD=1,

则AB=2,BD=2-x(0＜x＜2).

令y=tanA+2tanB==+

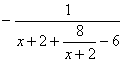=.又x+2+≥4.

当且仅当(x+2)²=8,即x=2-2时，取“=”.

∴当x=2-2时，y_min=.

此时，DB=2-（2-2）=4-2.

∴AD∶BD=.

答：取AD∶DB=1∶时，y_min=.