题目内容
在某校运动会中，甲、乙、丙三支足球队进行单循环赛（即每两队比赛一场）共赛三场，每场比赛胜者得3分，负者得0分，没有平局．在每一场比赛中，甲胜乙的概率为
，甲胜丙的概率为
，乙胜丙的概率为
；（1）求甲队获第一名且丙队获第二名的概率；
（2）设在该次比赛中，甲队得分为ξ，求ξ的分布列和数学期望．
【答案】分析：（1）设甲队获第一且丙队获第二为事件A，则甲赢两场，丙胜一场，由乘法公式求解即可；
（2）ξ可能的取值为0，3，6，分别计算出相应的概率，列出分布列，再由公式求出期望值即可；
解答：解：（1）设甲队获第一且丙队获第二为事件A，则P（A）=
=
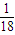
（2）ξ可能的取值为0，3，6；则
甲两场皆输：P（ξ=0）=（1-
）（1-
）=
甲两场只胜一场：P（ξ=3）=
×（1-
）+
×（1-
）=
甲两场皆胜：P（ξ=6）=
=
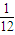
∴ξ的分布列为
Eξ=0×
+3×
+6×
=
点评：本题考查离散型随机事件的分布列与期望及方差，解题关键是正确理解“甲队获第一名且丙队获第二名”这个事件，且能用概率的乘法公式求出其概率，本题涉及到的公式较多，综合性较强．
（2）ξ可能的取值为0，3，6，分别计算出相应的概率，列出分布列，再由公式求出期望值即可；
解答：解：（1）设甲队获第一且丙队获第二为事件A，则P（A）=
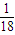
=（2）ξ可能的取值为0，3，6；则
甲两场皆输：P（ξ=0）=（1-
）（1-）=甲两场只胜一场：P（ξ=3）=
×（1-）+×（1-）=甲两场皆胜：P（ξ=6）=
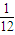
=∴ξ的分布列为
Eξ=0×
+3×+6×=点评：本题考查离散型随机事件的分布列与期望及方差，解题关键是正确理解“甲队获第一名且丙队获第二名”这个事件，且能用概率的乘法公式求出其概率，本题涉及到的公式较多，综合性较强．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，甲胜丙的概率为
，乙胜丙的概率为
的分布列和数学期望。
，求
，甲胜丙的概率为
，乙胜丙的概率为
的分布列和数学期望。