题目内容
已知函数
(1)求函数 的最大值,并写出
的最大值,并写出 取最大值
取最大值 时的取值集合;
时的取值集合;
(2)在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值.
(1) ,
,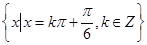 (2)
(2)
解析试题分析:(1)研究三角函数性质,首先将其化为基本三角函数形式,即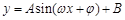 .利用两角和与差余弦公式、二倍角公式、配角公式,化简得
.利用两角和与差余弦公式、二倍角公式、配角公式,化简得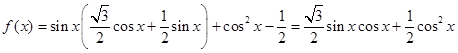
 ,再结合三角函数基本性质,可得函数
,再结合三角函数基本性质,可得函数 的最大值为
的最大值为 .
. 的取值集合为
的取值集合为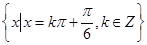 .(2)解三角形问题,利用正余弦定理进行边角转化. 因为
.(2)解三角形问题,利用正余弦定理进行边角转化. 因为 ,所以
,所以 已知一角及两夹边,利用余弦定理得
已知一角及两夹边,利用余弦定理得 .结合基本不等式,可得
.结合基本不等式,可得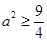 .
.
试题解析:(1)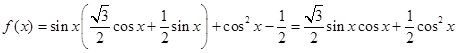
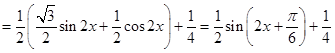 .
.
∴函数 的最大值为
的最大值为 .当
.当 取最大值时
取最大值时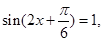
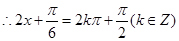 ,解得
,解得 .
.
故 的取值集合为
的取值集合为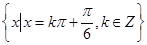 . (6分)
. (6分)
(2)由题意 ,化简得
,化简得 
 ,
, , ∴
, ∴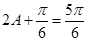 , ∴
, ∴
在 中,根据余弦定理,得
中,根据余弦定理,得 .
.
由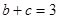 ,知
,知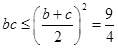 ,即
,即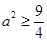 .
.
∴当 时,
时, 取最小值
取最小值 . (12分)
. (12分)
考点:两角和与差余弦公式、二倍角公式、配角公式, 余弦定理

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

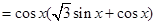 ,
,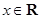 .
. ,
, .
. 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值. 的单调递增区间.
的单调递增区间. .
. 取得最大值时,求自变量
取得最大值时,求自变量 的集合;
的集合; ,其中
,其中 为常数.
为常数. 的周期;
的周期; 的最小值为
的最小值为 ,求
,求 的最大值及图像的对称轴方程.
的最大值及图像的对称轴方程. ,函数
,函数 .
. ,x为某三角形的内角,求
,x为某三角形的内角,求 时x的值;
时x的值; ,当函数
,当函数 取最大值时,求cos2x的值.
取最大值时,求cos2x的值. ,
, .
. 的值;(2)若
的值;(2)若 ,
,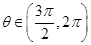 ,求
,求 .
. .
. 的最小正周期和值域;
的最小正周期和值域; 中,角
中,角 的对边分别为
的对边分别为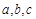 ,若
,若 且
且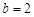 ,
,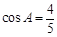 ,求
,求 和
和 .
. ),b=(
),b=( sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b. ]上的最大值和最小值.
]上的最大值和最小值.