题目内容
【题目】在各项均为正数的等比数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和. 设
项和. 设![]() ,当
,当![]() 最大时,求
最大时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)根据等比数列的通项公式,结合等差中项的定义列式,得2q4=2 q2+3×q3,解之得q=2(舍负),由此算出a1的值,即可得到数列{an}的通项公式;
(Ⅱ)根据对数的运算法则,结合an=2n﹣2算出bn=2n,从而得到{bn}构成等差数列,得出{bn}的前n项和Sn=n2-n,由此化简cn得cn=![]() .利用
.利用![]() 与0的大小,得到n≤5时c6>c5>…>c1,当n=6时,c6=c7;当n≥7时,c7>c8>…>cn,由此即可得到当cn最大时,求n的值为6或7.
与0的大小,得到n≤5时c6>c5>…>c1,当n=6时,c6=c7;当n≥7时,c7>c8>…>cn,由此即可得到当cn最大时,求n的值为6或7.
(Ⅰ)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]()
由![]() 得
得![]() ,
,
依题意,![]()
∴![]() 即
即![]()
解得![]() 或
或![]() (舍)
(舍)
所以![]() 的通项公式为
的通项公式为![]()
(Ⅱ)![]()
∵![]()
∴![]() 成等差数列
成等差数列
∴![]()
(法一)![]()
∵![]()
当![]() 时,
时,![]() 即
即![]()
当![]() 时,
时,![]() 即
即![]()
当![]() 时,
时,![]() 即
即![]()
∴![]()
∴ 当![]() 最大时,
最大时,![]() 或
或![]()
(法二)由![]() 得
得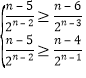
解得![]()
∴ 当![]() 最大时,
最大时,![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

