题目内容
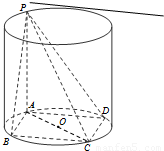
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.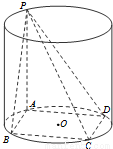
【答案】分析:根据底面圆的内接矩形的长和宽求出圆的半径,再由母线垂直于底面和“异面直线PB与CD所成的角为arctan2”求出母线长,代入圆柱的体积公式求出值.
解答: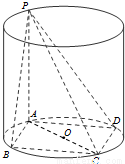 解:设圆柱下底面圆O的半径为r,连AC,由矩形ABCD内接于圆O,
解:设圆柱下底面圆O的半径为r,连AC,由矩形ABCD内接于圆O,
可知AC是圆O的直径,(2分)
∴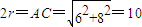 ,得r=5,(4分)
,得r=5,(4分)
由AB∥CD,可知∠PBA就是异面直线PB与CD所成的角,即∠PBA=arctan2,
∴tan∠PBA=2.(7分)
在直角三角形PAB中,PA=ABtan∠PBA=12,(9分)
∴圆柱的体积V=πr2•PA=π×52×12=300π.(12分)
点评:本题考查了圆柱的体积求法,主要根据圆内接矩形的性质、母线垂直于底面圆求出它的底面圆半径和母线,即关键求出半径和母线长即可.
解答:
 解:设圆柱下底面圆O的半径为r,连AC,由矩形ABCD内接于圆O,
解:设圆柱下底面圆O的半径为r,连AC,由矩形ABCD内接于圆O,可知AC是圆O的直径,(2分)
∴
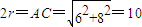 ,得r=5,(4分)
,得r=5,(4分)由AB∥CD,可知∠PBA就是异面直线PB与CD所成的角,即∠PBA=arctan2,
∴tan∠PBA=2.(7分)
在直角三角形PAB中,PA=ABtan∠PBA=12,(9分)
∴圆柱的体积V=πr2•PA=π×52×12=300π.(12分)
点评:本题考查了圆柱的体积求法,主要根据圆内接矩形的性质、母线垂直于底面圆求出它的底面圆半径和母线,即关键求出半径和母线长即可.

练习册系列答案
相关题目
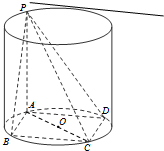 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.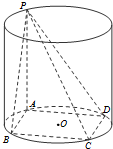 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.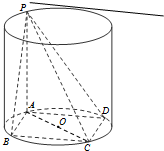 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.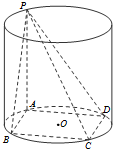
 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.