题目内容
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.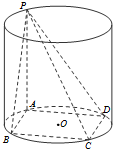

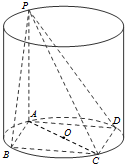
设圆柱下底面圆O的半径为r,连AC,由矩形ABCD内接于圆O,
可知AC是圆O的直径,(2分)
∴2r=AC=
| 62+82 |
由AB∥CD,可知∠PBA就是异面直线PB与CD所成的角,即∠PBA=arctan2,
∴tan∠PBA=2.(7分)
在直角三角形PAB中,PA=ABtan∠PBA=12,(9分)
∴圆柱的体积V=πr2?PA=π×52×12=300π.(12分)

练习册系列答案
相关题目
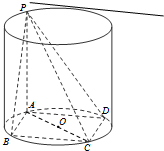 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.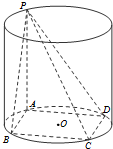 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.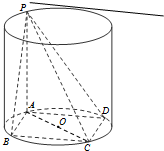 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.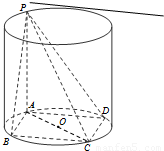 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.