题目内容
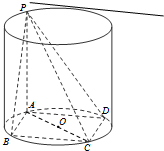 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
分析:建立空间直角坐标系A-xyz,求出向量
与
的坐标,设异面直线AC与PB所成角所成的角θ,
向量
与
的夹角为φ,利用两个向量的夹角公式,求出cosφ 的值,再取绝对值即得所求.
| AC |
| PB |
向量
| AC |
| PB |
解答: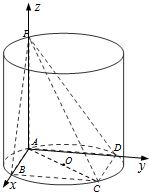 解:设圆柱下底面圆O的半径为r,由矩形ABCD内接于圆O,可知AC是圆O的直径,于是2r=AC=
解:设圆柱下底面圆O的半径为r,由矩形ABCD内接于圆O,可知AC是圆O的直径,于是2r=AC=
=10,得r=5,
又圆柱的体积V=25π•PA=300π,可得PA=12.
分别以直线AB,AD,AP为x,y,z轴,建立空间直角坐标系A-xyz,可得
=(6,8,0),
=(6,0,-12),
设异面直线AC与PB所成角所成的角θ,向量
与
的夹角为φ,
则cosθ=|cosφ|=
=
=
,
故异面直线AC与PB所成角的余弦值为
.
 解:设圆柱下底面圆O的半径为r,由矩形ABCD内接于圆O,可知AC是圆O的直径,于是2r=AC=
解:设圆柱下底面圆O的半径为r,由矩形ABCD内接于圆O,可知AC是圆O的直径,于是2r=AC=| 62+82 |
又圆柱的体积V=25π•PA=300π,可得PA=12.
分别以直线AB,AD,AP为x,y,z轴,建立空间直角坐标系A-xyz,可得
| AC |
| PB |
设异面直线AC与PB所成角所成的角θ,向量
| AC |
| PB |
则cosθ=|cosφ|=
|
| ||||
|
|
| 36 | ||
10×6
|
3
| ||
| 25 |
故异面直线AC与PB所成角的余弦值为
3
| ||
| 25 |
点评:本题考查异面直线所成的角的定义和求法,两个向量的数量积的定义,求出向量
与
的坐标是解题的关键,
注意cosθ 和cosφ的关系.
| AC |
| PB |
注意cosθ 和cosφ的关系.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
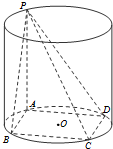 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,异面直线PB与CD所成的角为arctan2,求此圆柱的体积.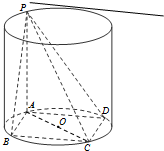 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.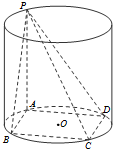
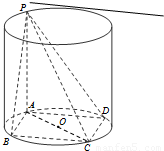 已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.
已知矩形ABCD内接于圆柱下底面的圆O,PA是圆柱的母线,若AB=6,AD=8,此圆柱的体积为300π,求异面直线AC与PB所成角的余弦值.