题目内容
18.设命题p:实数x满足x2-4ax+3a2<0,命题q:实数x满足log2x≤2.(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若a>0且?q是?p的充分不必要条件,求实数a的取值范围.
分析 (1)将a=1代入不等式,分别求出关于p,q的x的范围,结合p,q均为真,求出x的范围即可;
(2)根据p是q的充分不必要条件,得到关于a的不等式组,解出即可.
解答 解:(1)当a=1时,p:{x|1<x<3},q:{x|0<x≤4},(3分)
又p∧q为真,所以p真且q真,
由$\left\{{\begin{array}{l}{1<x<3}\\{0<x≤4}\end{array}}\right.$,得1<x<3
所以实数a的取值范围为(1,3)(5分)
(2)因为¬q是¬p的充分不必要条件,
所以p是q的充分不必要条件,(7分)
又p:{x|a<x<3a},q:{x|0<x≤4},
所以$\left\{{\begin{array}{l}{a>0}\\{\;}\\{3a≤4}\end{array}}\right.$,解得$0<a≤\frac{4}{3}$
所以实数a的取值范围为$({0,\;\frac{4}{3}}]$(10分).
点评 本题考查了充分必要条件,考查复合命题的判断,集合的包含关系,是一道中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
6.已知$f(x)={x^{\frac{1}{3}}}-{({\frac{1}{2}})^x}$,其零点所在区域为( )
| A. | $({0,\frac{1}{3}})$ | B. | $({\frac{1}{3},\frac{1}{2}})$ | C. | $({\frac{1}{2},1})$ | D. | (2,3) |
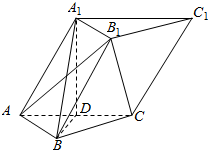 如图,在各棱长均相等的三棱柱ABC-A1B1C1中,∠A1AC=60°,D为AC的中点.
如图,在各棱长均相等的三棱柱ABC-A1B1C1中,∠A1AC=60°,D为AC的中点.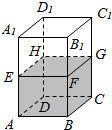 如图所示,在透明塑料制成的长方体容器ABCD-A1B1C1D1灌进一些水,将容器底面的一边BC固定于地面上,再将容器倾斜,随着倾斜程度的不同,有以下命题:
如图所示,在透明塑料制成的长方体容器ABCD-A1B1C1D1灌进一些水,将容器底面的一边BC固定于地面上,再将容器倾斜,随着倾斜程度的不同,有以下命题: