题目内容
9．
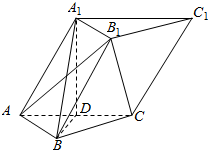如图，在各棱长均相等的三棱柱ABC-A1B1C1中，∠A1AC=60°，D为AC的中点．（1）求证：B1C∥平面A1BD；
（2）求证：平面ABB1A1⊥平面AB1C．
分析 （1）连接AB1和A1B，交于E，连接DE，运用中位线定理和线面平行的判定定理，即可得证；
（2）运用菱形的对角线垂直和线面垂直的判断和性质，可得A1B⊥平面AB1C，再由面面垂直的判定定理，即可得证．
解答 
证明：（1）连接AB1和A1B，交于E，连接DE，
由D，E分别为AC，A1B的中点，可得DE∥B1C，
由DE?平面A1BD，B1C?平面A1BD，
即有B1C∥平面A1BD；
（2）由菱形ABB1A1，可得AB1⊥A1B，
∠A1AC=60°，D为AC的中点，可得A1D⊥AC，
又BD⊥AC，则AC⊥平面A1BD，
即有AC⊥A1B，又AB1⊥A1B，
则A1B⊥平面AB1C，
而A1B?平面ABB1A1，则平面ABB1A1⊥平面AB1C．
点评 本题考查线面平行和面面垂直的判定，注意运用线面平行和面面垂直的判定定理，考查空间线面位置关系的转化，属于中档题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19．下列函数中满足在（-∞，0）是单调递增的是（ ）
| A． | f（x）=$\frac{1}{x+2}$ | B． | f（x）=-（x+1）2 | C． | f（x）=1+2x2 | D． | f（x）=-|x| |
17．下列说法中正确的个数有（ ）
①两平面平行，夹在两平面间的平行线段相等；
②两平面平行，夹在两平面间的相等的线段平行；
③两条直线被三个平行平面所截，截得的线段对应成比例；
④如果夹在两平面间的三条平行线段相等，那么这两个平面平行．
①两平面平行，夹在两平面间的平行线段相等；
②两平面平行，夹在两平面间的相等的线段平行；
③两条直线被三个平行平面所截，截得的线段对应成比例；
④如果夹在两平面间的三条平行线段相等，那么这两个平面平行．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
4．已知△ABC的外接圆半径为1，圆心为O，且3$\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow{0}$，则△ABC的面积为（ ）
| A． | $\frac{8}{5}$ | B． | $\frac{7}{5}$ | C． | $\frac{6}{5}$ | D． | $\frac{4}{5}$ |
1．命题“设 a、b、c∈R，若ac2＞bc2 则 a＞b”的原命题、逆命题、否命题中，真命题的个数是（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |