题目内容
在 中,
中, 分别是角
分别是角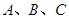 所对的边,且
所对的边,且 .
.
(1)求角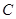 ;
;
(2)若 ,求
,求 的周长
的周长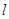 的取值范围.
的取值范围.
 中,
中, 分别是角
分别是角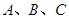 所对的边,且
所对的边,且 .
.(1)求角
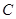 ;
;(2)若
 ,求
,求 的周长
的周长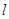 的取值范围.
的取值范围.(1)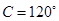 ;(2)周长
;(2)周长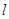 的取值范围是
的取值范围是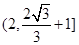 .
.
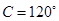 ;(2)周长
;(2)周长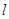 的取值范围是
的取值范围是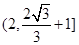 .
.试题分析:(1)条件中的等式
 是边角的关系,因此可以考虑采用正弦定理进行边角互化,统一转化为边之间的关系,结合余弦定理的变式,即可求得
是边角的关系,因此可以考虑采用正弦定理进行边角互化,统一转化为边之间的关系,结合余弦定理的变式,即可求得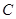 的大小:
的大小: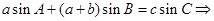
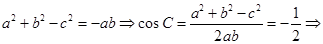
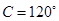 ;
;由题意可知,求周长
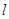 的取值范围只需求得
的取值范围只需求得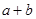 的取值范围即可,而根据(1)中所得的边之间的关系式结合基本不等式即可求得
的取值范围即可,而根据(1)中所得的边之间的关系式结合基本不等式即可求得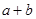 的取值范围:
的取值范围: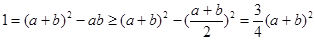
即
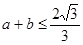 ,又由
,又由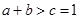 ,从而可知周长
,从而可知周长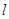 的取值范围是
的取值范围是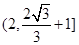 .
.试题解析:(1)∵
 ,∴
,∴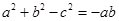 , 3分
, 3分∴
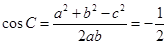 , 6分
, 6分又∵
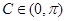 ,∴
,∴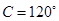 ; 7分
; 7分(2)由(1)得:
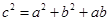 , 9分
, 9分又∵
 ,故
,故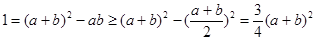 , 11分
, 11分∴
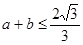 , 12分 又∵
, 12分 又∵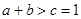 , 13分
, 13分∴
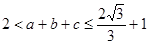 ,即
,即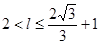 ,∴周长
,∴周长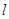 的取值范围是
的取值范围是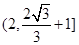 14分
14分
练习册系列答案
相关题目
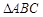 中,已知
中,已知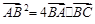 .
.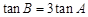 ;(2)若
;(2)若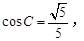 AB=4 ,求
AB=4 ,求 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,且满足
,且满足
 ,求
,求 .
.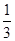 ,求B.
,求B.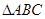 中,角
中,角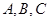 的对边分别是
的对边分别是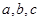 ,已知
,已知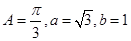 ,则
,则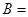 ( )
( )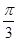
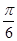
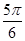
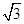 ,则AC=
,则AC= 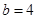 ,
,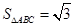 ,则
,则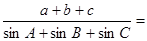 .
.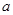 、
、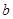 、c,且
、c,且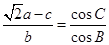 ,则B的大小为_________.
,则B的大小为_________.