题目内容
已知点P是△ABC所在平面内的一点,且满足3
+5
+2
=
,设△ABC的面积为S,则△PAC的面积为( )
| PA |
| PB |
| PC |
| 0 |
分析:取AB中点M,取BC中点N,根据已知3
+5
+2
=
可得6
+4
=
,即P,M,N三点共线,进而根据分析出△ABC与△PAC高的关系,得到答案.
| PA |
| PB |
| PC |
| 0 |
| PM |
| PN |
| 0 |
解答: 解:∵3
解:∵3
+5
+2
=
,
∴3(
+
)+2(
+
)=
取AB中点M,取BC中点N
+
=2
,
+
=
∴6
+4
=
又∵MN是三角形ABC中位线,
∴P在MN上
∴三角形PAC的面积等三角形ABC面积的一半
故选B
 解:∵3
解:∵3| PA |
| PB |
| PC |
| 0 |
∴3(
| PA |
| PB |
| PB |
| PC |
| 0 |
取AB中点M,取BC中点N
| PA |
| PB |
| PM |
| PB |
| PC |
| PN |
∴6
| PM |
| PN |
| 0 |
又∵MN是三角形ABC中位线,
∴P在MN上
∴三角形PAC的面积等三角形ABC面积的一半
故选B
点评:本题考查的知识点是向量在几何中的应用,其中根据已知结合向量共线的充要条件分析出P在三角形的中位线上是解答的关键.

练习册系列答案
相关题目
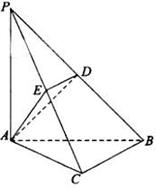
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)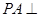 底面
底面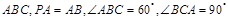 ,点
,点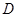 ,
,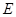 分别在棱
分别在棱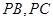 上,且
上,且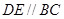 。
。
。
。 
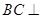 平面
平面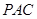 ;
;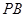 的中点时,求
的中点时,求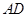 与平面
与平面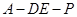 为直二面角?并说明理由.
为直二面角?并说明理由. 的解集是 .
的解集是 .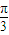 ),则|PQ|的最小值为 .
),则|PQ|的最小值为 .
 的解集是 .
的解集是 .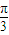 ),则|PQ|的最小值为 .
),则|PQ|的最小值为 .