题目内容
设A、B、C是△ABC的三个内角,且sin2B + sin2C = sin2A +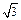 sinBsinC,则2sinBcosC – sin (B – C)的值为( )
sinBsinC,则2sinBcosC – sin (B – C)的值为( )
A.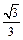 B.
B.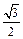 C.
C.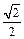 D.
D.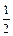
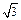 sinBsinC,则2sinBcosC – sin (B – C)的值为( )
sinBsinC,则2sinBcosC – sin (B – C)的值为( )A.
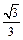 B.
B.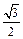 C.
C.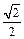 D.
D.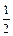
D
由sin2B + sin2C = sin2A +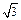 sinBsinC可得sinA =
sinBsinC可得sinA =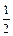
而2sinBcosC– sin (B – C) =" sin" (B + C) = sinA.故选D.
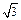 sinBsinC可得sinA =
sinBsinC可得sinA =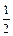
而2sinBcosC– sin (B – C) =" sin" (B + C) = sinA.故选D.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
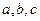 分别为角A,B,C的对边,设
分别为角A,B,C的对边,设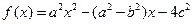 ,(1)若
,(1)若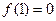 ,且B-C=
,且B-C=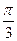 ,求角C.(2)若
,求角C.(2)若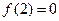 ,求角C的取值范围.
,求角C的取值范围. 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且 ∥
∥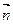
 若
若 ,求
,求 的最大值。
的最大值。 中,若
中,若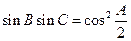 ,则此三角形为___
,则此三角形为___ ___.
___.
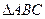 的三个顶点分别是
的三个顶点分别是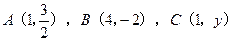 ,
,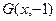 ,则
,则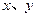 的值分别是( )
的值分别是( )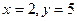
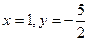
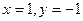

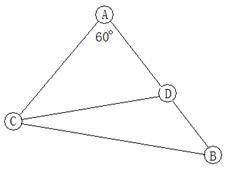
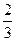 ,那么PC与平面
,那么PC与平面 ABC所成的角是( )
ABC所成的角是( )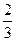
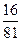
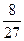
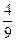
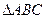 中,三个内角
中,三个内角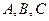 所对的边分别是
所对的边分别是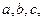 已知
已知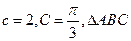 的面积等于
的面积等于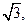
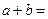 ____★____.
____★____.