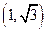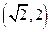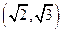题目内容
(本题满分12分)在△ABC中,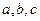 分别为角A,B,C的对边,设
分别为角A,B,C的对边,设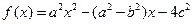 ,(1)若
,(1)若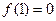 ,且B-C=
,且B-C=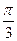 ,求角C.(2)若
,求角C.(2)若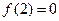 ,求角C的取值范围.
,求角C的取值范围.
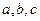 分别为角A,B,C的对边,设
分别为角A,B,C的对边,设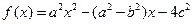 ,(1)若
,(1)若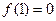 ,且B-C=
,且B-C=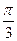 ,求角C.(2)若
,求角C.(2)若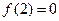 ,求角C的取值范围.
,求角C的取值范围.(1)C=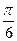
(2)0<C≤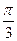
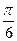
(2)0<C≤
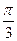
解;(1)由f(1)=0,得a2-a2+b2-4c2=0, ∴b= 2c…………(1分).
又由正弦定理,得b= 2RsinB,c=2RsinC,将其代入上式,得sinB=2sinC…………(2分)
∵B-C=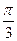 ,∴B=
,∴B=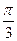 +C,将
+C,将 其代入上式,得sin(
其代入上式,得sin(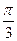 +C)=2sinC……………(3分)
+C)=2sinC……………(3分)
∴sin(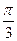 )cosC + cos
)cosC + cos 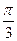 sinC =2sinC,整理得,
sinC =2sinC,整理得,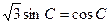 …………(4分)
…………(4分)
∴tanC=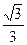 ……………(5分)
……………(5分)
∵角C是三角形的内角,∴C=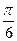 …………………(6分)
…………………(6分)
(2)∵f(2)=0,∴4a2-2a2+2b2-4c2=0,即a2+b2-2c2=0……………(7分)
由余弦定理,得cosC=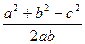 ……………………(8分)
……………………(8分)
=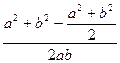
∴cosC=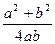
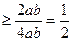 (当且仅当a=b时取等号)…………(10分)
(当且仅当a=b时取等号)…………(10分)
∴cosC≥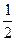 ,
,
∠C是锐角,又∵余弦函数在(0,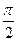 )上递减,∴.0<C≤
)上递减,∴.0<C≤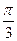 ………………(12分)
………………(12分)
又由正弦定理,得b= 2RsinB,c=2RsinC,将其代入上式,得sinB=2sinC…………(2分)
∵B-C=
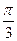 ,∴B=
,∴B=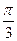 +C,将
+C,将 其代入上式,得sin(
其代入上式,得sin(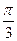 +C)=2sinC……………(3分)
+C)=2sinC……………(3分)∴sin(
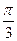 )cosC + cos
)cosC + cos 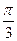 sinC =2sinC,整理得,
sinC =2sinC,整理得,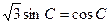 …………(4分)
…………(4分)∴tanC=
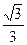 ……………(5分)
……………(5分)∵角C是三角形的内角,∴C=
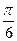 …………………(6分)
…………………(6分)(2)∵f(2)=0,∴4a2-2a2+2b2-4c2=0,即a2+b2-2c2=0……………(7分)
由余弦定理,得cosC=
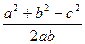 ……………………(8分)
……………………(8分)=
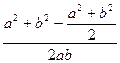
∴cosC=
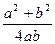
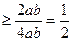 (当且仅当a=b时取等号)…………(10分)
(当且仅当a=b时取等号)…………(10分)∴cosC≥
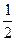 ,
,∠C是锐角,又∵余弦函数在(0,
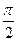 )上递减,∴.0<C≤
)上递减,∴.0<C≤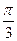 ………………(12分)
………………(12分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且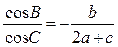 。
。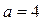 ,
,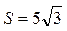 ,求
,求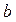 的值。
的值。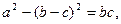
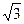 ,角B等于x,周长为y,求函数
,角B等于x,周长为y,求函数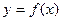 的取值范围.
的取值范围.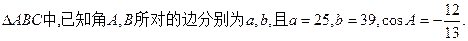
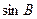 的值;
的值;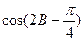 的值.
的值.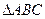 中,
中,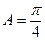 ,
,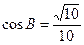 .
.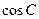 ;
;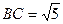 ,求
,求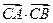 的值.
的值.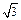 sinBsinC,则2sinBcosC – sin (B – C)的值为( )
sinBsinC,则2sinBcosC – sin (B – C)的值为( )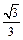 B.
B.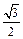 C.
C.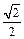 D.
D.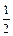
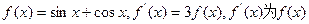 的导数,则
的导数,则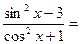 ( )
( )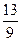
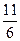
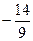
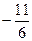 F
F 中,
中, ,那么
,那么 为( )
为( )
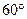
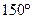

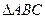 中,
中, 若
若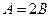 ,则
,则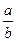 的取值范围是
的取值范围是