题目内容
已知等比数列{xn}的各项为不等于1的正数,数列{yn}满足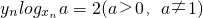 ,设y3=18,y6=12.
,设y3=18,y6=12.
(1)求数列{yn}的前多少项和最大,最大值为多少?
(2)试判断是否存在自然数M,使当n>M时,xn>1恒成立?若存在,求出相应的M,若不存在,请说明理由;
(3)令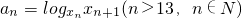 ,试判断数列{an}的增减性?
,试判断数列{an}的增减性?
解:(1)由已知得:yn=2logaxn设等比数列{xn}的公比为q(q≠1)
由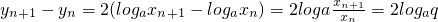 得{yn}为等差数列,设公差为d
得{yn}为等差数列,设公差为d
∵y3=18,y6=12,∴d=-2;∴yn=y3+(n-3)d=24-2n
设前k项为最大,则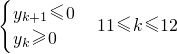 y12=0
y12=0
∴前11项和前12项和为最大,其和为132
(2)xn=a12-n,n∈N*?;若xn>1,则a12-n>1?
当a>1时,n<12,显然不成立;当0<a<1时,n>12
∴存在M=12,13,14,…,?当n>M时,xn>1
(3)an=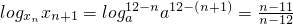
∵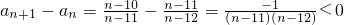
∴an+1<an∴n>13时数列{an}为递减数列
分析:(1)先根据等差数列的定义判定数列{yn},然后根据y3=18,y6=12可求出首项和公差,设前k项为最大,则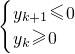 ,可求出k的值,从而求出所求;
,可求出k的值,从而求出所求;
(2)讨论a与1的大小,然后解指数不等式,从而求出适合条件的M;
(3)先求出数列{an}的通项公式,然后判定an+1-an的符号,可得数列的单调性.
点评:本题主要考查了等差数列的判定,以及恒成立问题和数列单调性的判定,属于中档题.
由
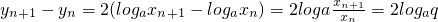 得{yn}为等差数列,设公差为d
得{yn}为等差数列,设公差为d∵y3=18,y6=12,∴d=-2;∴yn=y3+(n-3)d=24-2n
设前k项为最大,则
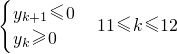 y12=0
y12=0∴前11项和前12项和为最大,其和为132
(2)xn=a12-n,n∈N*?;若xn>1,则a12-n>1?
当a>1时,n<12,显然不成立;当0<a<1时,n>12
∴存在M=12,13,14,…,?当n>M时,xn>1
(3)an=
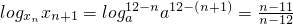
∵
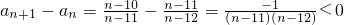
∴an+1<an∴n>13时数列{an}为递减数列
分析:(1)先根据等差数列的定义判定数列{yn},然后根据y3=18,y6=12可求出首项和公差,设前k项为最大,则
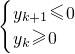 ,可求出k的值,从而求出所求;
,可求出k的值,从而求出所求;(2)讨论a与1的大小,然后解指数不等式,从而求出适合条件的M;
(3)先求出数列{an}的通项公式,然后判定an+1-an的符号,可得数列的单调性.
点评:本题主要考查了等差数列的判定,以及恒成立问题和数列单调性的判定,属于中档题.

练习册系列答案
相关题目
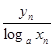 =2(a>0,且a≠1),设y3=18, y6=12.
=2(a>0,且a≠1),设y3=18, y6=12.
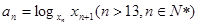 试比较
试比较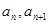 的大小.
的大小.