题目内容
已知圆C1: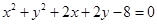 与圆C2:
与圆C2: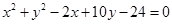 相交于A、B两点,
相交于A、B两点,
(1)求公共弦AB所在的直线方程;
(2)求圆心在直线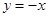 上,且经过A、B两点的圆的方程.
上,且经过A、B两点的圆的方程.
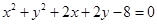 与圆C2:
与圆C2: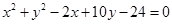 相交于A、B两点,
相交于A、B两点,(1)求公共弦AB所在的直线方程;
(2)求圆心在直线
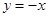 上,且经过A、B两点的圆的方程.
上,且经过A、B两点的圆的方程. (1)x-2y+4=0.(2)⊙M:(x+3)2+(y-3)2=10.
(1)两圆方程作差,可得两相交圆公共弦所在的直线方程.
(2)在(1)的基础上,求出AB的垂直平分线方程再与直线y=-x联立可得交点坐标即圆心M的坐标,然后再由圆C1和圆C2的方程联立可解出A,B的坐标,从而可求出半径|MA|的值,进而写出圆M的方程.
(1)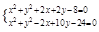 ⇒x-2y+4=0.
⇒x-2y+4=0.
(2)由(1)得x=2y-4,代入x2+y2+2x+2y-8=0中得:y2-2y=0.
∴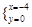 或
或 ,即A(-4,0),B(0,2),
,即A(-4,0),B(0,2),
又圆心在直线y=-x上,设圆心为M(x,-x),则|MA|=|MB|,解得M(-3,3),∴⊙M:(x+3)2+(y-3)2=10.
(2)在(1)的基础上,求出AB的垂直平分线方程再与直线y=-x联立可得交点坐标即圆心M的坐标,然后再由圆C1和圆C2的方程联立可解出A,B的坐标,从而可求出半径|MA|的值,进而写出圆M的方程.
(1)
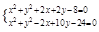 ⇒x-2y+4=0.
⇒x-2y+4=0.(2)由(1)得x=2y-4,代入x2+y2+2x+2y-8=0中得:y2-2y=0.
∴
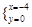 或
或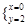 ,即A(-4,0),B(0,2),
,即A(-4,0),B(0,2),又圆心在直线y=-x上,设圆心为M(x,-x),则|MA|=|MB|,解得M(-3,3),∴⊙M:(x+3)2+(y-3)2=10.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
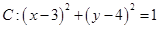 和两点
和两点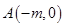 ,
,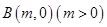 ,若圆
,若圆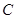 上存在点
上存在点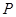 ,使得
,使得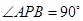 ,则
,则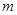 的最大值为( )
的最大值为( )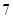
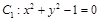 和
和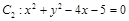 的位置关系是( )
的位置关系是( )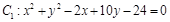 与
与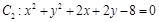 公共弦的长为 .
公共弦的长为 .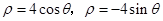 .
.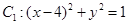 ,圆
,圆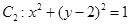 ,动点
,动点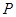 到圆
到圆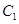 ,
,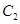 上点的距离的最小值相等.
上点的距离的最小值相等.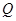 ,使得点
,使得点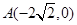 的距离减去点
的距离减去点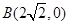 的距离的差为
的距离的差为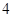 ,如果存在求出
,如果存在求出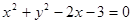 与圆
与圆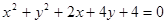 的位置关系是
的位置关系是