题目内容
11.在单位圆上有两个动点P,Q,它们同时从点A(1,0)出发沿圆周运动,已知点P按逆时针方向每秒转$\frac{π}{3}$,点Q按顺时针方向每秒转$\frac{π}{6}$,试求它们从出发后到第五次相遇时各自走过的弧长.分析 设出第5次相遇经历的时间,然后,建立等式,求解时间,利用弧长公式即可得解.
解答 解:设它们出发后第5次相遇,用的时间为t秒,则$\frac{π}{6}$t+$\frac{π}{3}$t=10π,
解得:t=20(秒),
此时动点P所走过的弧度为:$\frac{π}{3}$×20=$\frac{20π}{3}$,
动点N所走过的弧度为:$\frac{π}{6}×20$=$\frac{10π}{3}$.
点评 本题重点考查了三角函数的图象与性质、三角公式、弧长公式等知识,属于中档题,解题关键是灵活运用弧长公式进行求解.

练习册系列答案
相关题目
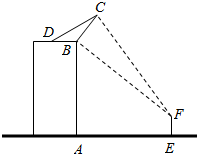 如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.
如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.