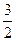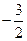题目内容
已知抛物线C1:x2=8y和圆C2:x2+(y-2)2=4,直线l过C1焦点,且与C1,C2交于四点,从左到右依次为A,B,C,D,则
•
=______.
| AB |
| CD |
∵抛物线C1:x2=8y的焦点为F(0,2),圆C2:x2+(y-2)2=4的圆心为(0,2),∴直线l过圆C2的圆心.
设直线l的方程为y=kx+2,A(x1,y1),D(x2,y2),联立
,得y2-(4+8k2)y+4=0,
∴y1•y2=4
又根据抛物线定义得|AF|=y1+
,FD=y2+
,∴AF=y1+2,FD=y2+2
则
•
=
|•|
|=(AF-BF)(FD-CF)
=(y1+2-2)(y2+2-2)=y1•y2=4.
故答案为4
设直线l的方程为y=kx+2,A(x1,y1),D(x2,y2),联立
|
∴y1•y2=4
又根据抛物线定义得|AF|=y1+
| p |
| 2 |
| p |
| 2 |
则
| AB |
| CD |
| |AB |
| CD |
=(y1+2-2)(y2+2-2)=y1•y2=4.
故答案为4

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
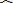
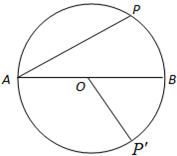
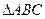 中,设
中,设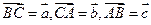 ,则
,则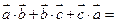 ( )
( )