题目内容
.已知矩阵A=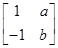 ,A的一个特征值λ=2,其对应的特征向量是α1=
,A的一个特征值λ=2,其对应的特征向量是α1=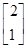 .设向量β=
.设向量β=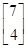 ,试计算A5β的值.
,试计算A5β的值.
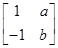 ,A的一个特征值λ=2,其对应的特征向量是α1=
,A的一个特征值λ=2,其对应的特征向量是α1=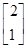 .设向量β=
.设向量β=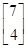 ,试计算A5β的值.
,试计算A5β的值.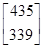
由题设条件可得,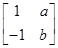
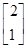 =2
=2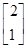 ,即
,即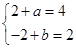 解得
解得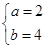 得矩阵A=
得矩阵A=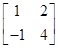 .
.
矩阵A的特征多项式为f(λ)=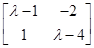 =λ2-5λ+6,令f(λ)=0,解得
=λ2-5λ+6,令f(λ)=0,解得
λ1=2,λ2=3.
当λ1=2时,得α1=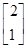 ;当λ2=3时,得α2=
;当λ2=3时,得α2=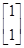 ,
,
由β=mα1+nα2,得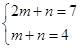 得m=3,n=1,
得m=3,n=1,
∴A5β=A5(3α1+α2)=3(A5α1)+A5α2=3(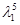 α1)+
α1)+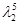 α2=3×25
α2=3×25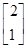 +35
+35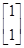 =
=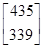
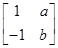
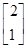 =2
=2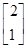 ,即
,即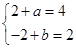 解得
解得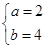 得矩阵A=
得矩阵A=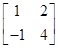 .
.矩阵A的特征多项式为f(λ)=
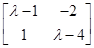 =λ2-5λ+6,令f(λ)=0,解得
=λ2-5λ+6,令f(λ)=0,解得λ1=2,λ2=3.
当λ1=2时,得α1=
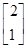 ;当λ2=3时,得α2=
;当λ2=3时,得α2=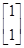 ,
,由β=mα1+nα2,得
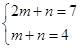 得m=3,n=1,
得m=3,n=1,∴A5β=A5(3α1+α2)=3(A5α1)+A5α2=3(
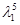 α1)+
α1)+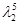 α2=3×25
α2=3×25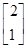 +35
+35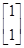 =
=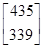

练习册系列答案
相关题目
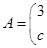
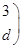 ,若矩阵
,若矩阵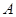 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为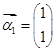 ,属于特征值1的一个特征向量
,属于特征值1的一个特征向量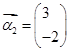 .
.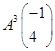
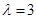 及对应的一个特征向量
及对应的一个特征向量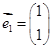 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点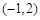 变换成
变换成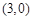 ,求矩阵M.
,求矩阵M.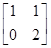 有特征向量为e1=
有特征向量为e1=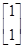 ,e2=
,e2=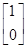 ,
,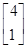 ,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.
,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.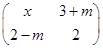 总存在特征向量,求m的取值范围.
总存在特征向量,求m的取值范围.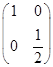 .
. ,3)在该变换作用下的象.
,3)在该变换作用下的象.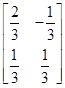 ,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积.
,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积.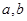 满足
满足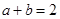 ,则行列式
,则行列式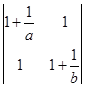 的最小值为 .
的最小值为 .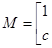
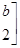 有特征值
有特征值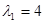 及对应的一个特征向量
及对应的一个特征向量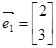 ,求曲线
,求曲线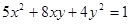 在
在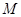 的作用下的新曲线方程.
的作用下的新曲线方程.