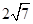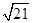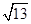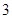题目内容
在△ABC中,角A,B,C所对的边长分别为a,b,c.若C=120°,c=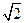 a,则( )
a,则( )
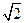 a,则( )
a,则( )| A.a>b |
| B.a<b |
| C.a=b |
| D.a与b的大小关系不能确定 |
A
方法一:由余弦定理得2a2=a2+b2-2abcos120°,
∴b2+ab-a2=0,
即(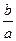 )2+
)2+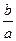 -1=0
-1=0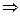
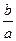 =
=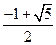 <1,故b<a.
<1,故b<a.
方法二:由余弦定理得2a2=a2+b2-2abcos120°,
∴b2+ab-a2=0,
即b2=a2-ab=a(a-b)>0,∴a>b.
∴b2+ab-a2=0,
即(
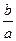 )2+
)2+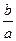 -1=0
-1=0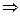
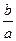 =
=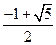 <1,故b<a.
<1,故b<a.方法二:由余弦定理得2a2=a2+b2-2abcos120°,
∴b2+ab-a2=0,
即b2=a2-ab=a(a-b)>0,∴a>b.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目

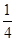 (b2+c2-a2),则A=( )
(b2+c2-a2),则A=( )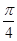
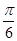
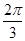
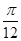
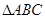 中,
中,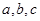 分别是
分别是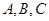 所对的边,
所对的边,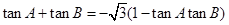 ,
,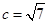 ,三角形的面积为
,三角形的面积为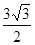 ,
,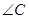 的大小; (2)求
的大小; (2)求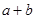 的值.
的值.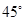 ,与观测站A距离
,与观测站A距离 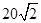 海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北
海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北 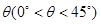 的C处,且
的C处,且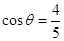 ,已知A、C两处的距离为10海里,则该货船的船速为海里/小时___________.
,已知A、C两处的距离为10海里,则该货船的船速为海里/小时___________.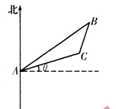
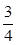 B.
B.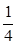 C.
C. D.
D.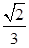
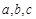 分别为角
分别为角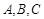 所对的边,若
所对的边,若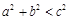 ,则△ABC的形状为( )
,则△ABC的形状为( )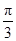 ,且sinA∶sinC=3∶1,则b∶c的值为 .
,且sinA∶sinC=3∶1,则b∶c的值为 . 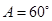 ,
,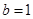 ,△
,△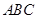 的面积为
的面积为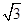 ,则边
,则边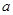 的值为
的值为